Предыдущая страница реферата | 13  14  15  16  17  18  19  20  21  22  23 | Следующая страница реферата

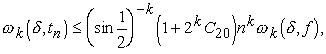(5.4)

и

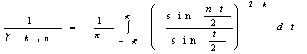(5.5)

Предварительные замечания. Неравенства (5.2) и (5.4) предпочтительнее для больших , а (5.3)-для малых. Если , то (5.2) сильнее, чем (5.4); однако (5.4) имеет более симметричную форму и часто удобнее в приложениях.

Доказательство. Докажем (5.2). Пользуясь (2.1), (2.2) и (5.1), имеем

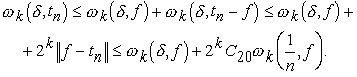
Докажем (5.5). Положим в (5.2) . Тогда получим :

после чего (4.5) даёт (5.5).

(5.3) следует из (5.5) в силу (2.11).

Остаётся доказать (5.4). Пусть сперва . Тогда из (5.4) следует:

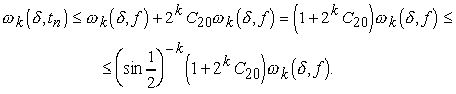
Рассмотрим, наконец, случай . Из неравенства (2.7) выводим

Подставляя эту оценку в (5.3), получаем (5.4) для .

Таким образом, теорема полностью доказана.

Следствие 3.1. Пусть для некоторого натурального k и любого натурального n

(5.6)

Тогда для любого >0

(5.7)

равномерно относительно n.

Следствие 3.2. Пусть для некоторого натурального k и любого натурального n

Тогда

(5.8)

Рекомендуем скачать другие рефераты по теме: аристотель реферат, международный реферат.



Предыдущая страница реферата | 13  14  15  16  17  18  19  20  21  22  23 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки