Предыдущая страница реферата | 16  17  18  19  20  21  22  23  24  25  26 | Следующая страница реферата

левая часть этого неравенства не зависит от n, а поэтому

и лемма доказана.

Для получения хороших оценок обычно достаточно взять . Однако на исключена возможность, что в некоторых случаях другой выбор может оказаться предпочтительнее.

Теорема 7. Пусть k-натуральное число, функция не убывает и

(6.4)

Для того чтобы , необходимо и достаточно выполнение условия

(6.5)

Доказательство. Необходимость условия (6.5) вытекает из следствия 3.2. Установим его достаточность, для чего воспользуемся леммой 9. Получаем:

Положим здесь ; тогда для будем иметь и поэтому

и теорема доказана.

Отметим два следствия из этой теоремы.

Следствие 7.1. Пусть k-натуральное число, функция не убывает и

(6.6)

Для того чтобы , необходимо и достаточно выполнение условия

(6.7)

Следствие 7.2. Пусть k-натуральное число и Если

и

(6.8)

то

равномерно относительно n.

Это вытекает из теорем 7 и 6.

Теорема 7 показывает, что нужно добавить к условию (6.4), чтобы получить . Теперь мы получим оценки для , исходя только из условий вида (6.4). Попутно выясняется, что при некоторых дополнительных ограничениях на функцию условие (6.5) становится излишним. Суть дела в том, что при этих ограничениях (6.4) влечёт (6.5).

Лемма 10. Пусть

(6.9)

где . Тогда для любого натурального k

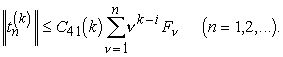(6.10)

Доказательство. Зафиксируем натуральное число n, определим натуральное p из условий

и построим последовательность номеров положив

Для оценки представим в таком виде:

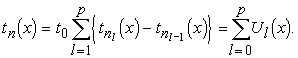
Так как , то отсюда

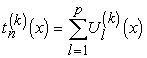
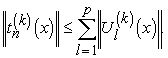(6.11)

Оценим Ul(k). Имеем для l=1,2,...,p

откуда

Но есть тригонометрический полином порядка не выше nl. Поэтому по неравенству С.Н. Бернштейна,

(6.12)

Заметим теперь, что, в силу определения последовательности {nl},

и для

Поэтому, пользуясь ещё монотонностью последовательности {Fn}2 находим, что для

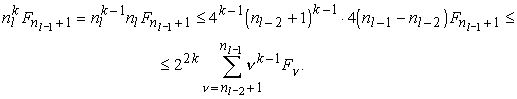(6.13)

Рекомендуем скачать другие рефераты по теме: аристотель реферат, международный реферат.



Предыдущая страница реферата | 16  17  18  19  20  21  22  23  24  25  26 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки