Предыдущая страница реферата | 16  17  18  19  20  21  22  23  24  25  26 | Следующая страница реферата

Тогда существует такая константа с>0, что

(7.2)

Доказательство. Согласно (7.1), найдутся две такие константы С60>0 и C61>0, что

(7.3)

Последнее из этих неравенств, теорема 1 и теорема 3 влекут неравенство

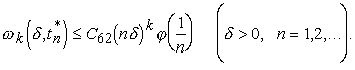(7.4)

В силу (2.1) и (2.2), имеем

Отсюда

Пользуясь (7.3) и (7.4), находим, далее

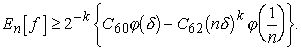(7.5)

Вспомним теперь, что . Это даёт нам для

Подставляя эту оценку в (7.5), получаем

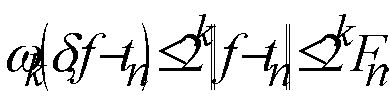(7.6)

Мы можем без ограничения общности считать, что здесь . Положим в (7.6)

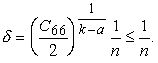
Тогда получим окончательно

и лемма доказана.

Основная теорема. Пусть . Для того чтобы

(7.7)

необходимо, чтобы для всех натуральных , и достаточно, чтобы для некоторого натурального

. (7.8)

Доказательство. Пусть имеет место (7.7), т.е. найдутся две положительные константы С67 и С68, для которых

(7.9)

Тогда, по теореме 1 и в силу первой половины неравенства (7.9), для любого k имеем

т.е.

Отсюда, в силу ,

и если , то, ввиду монотонности и ,

Далее, из второй половины неравенства (7.9) и теоремы 9 вытекает существование константы С72 такой, что для любого

Этим заканчивается доказательство необходимости условия (7.8).

Пусть имеет место (7.8):

(7.10)

с С73>0. Тогда по теореме 1 и в силу второй половины неравенства (6.10),

а по лемме 11,

где С77>0.

Таким образом, установлена достаточность условия (7.8), и основная теорема полностью доказана.

Приведём в заключение обобщение леммы 11 на тот случай, когда оценки сверху и снизу имеют разные порядки.

Теорема 12. Пусть и

(7.11)

Тогда

Рекомендуем скачать другие рефераты по теме: аристотель реферат, международный реферат.



Предыдущая страница реферата | 16  17  18  19  20  21  22  23  24  25  26 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки