Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

В §7 доказывается основная теорема. Мы даём здесь же оценку En[f] снизу, если

.

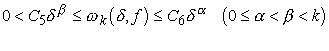Именно, тогда

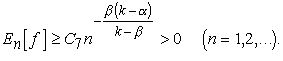
Случай =0 установлен С.Н.Бернштейном [3].

В §8 мы рассматриваем несколько решений задач с использованием различных модулей непрерывности.

§1. Некоторые вспомогательные определения.

В работе рассматриваются непрерывные функции f с периодом 2 и их приближение тригонометрическими полиномами. Через tn(x) обозначается тригонометрический полином порядка не выше n, а через tn*(x)=tn*(x,f)-тригонометрический полином, наименее уклоняющийся от f среди всех tn(x). Мы полагаем и пишем

Введём ряд определений.

Определение 1. При каждом фиксированном классом Липшица порядка  называется множество всех непрерывных функция f, модуль непрерывности каждой из которых удовлетворяет условию

где С8-какая-нибудь положительная постоянная, которая не зависит от  и которая, вообще говоря, является различной для разных функций. Этот класс обозначается H или Lip 

Определение 2. Обозначим при фиксированном натуральном r через W(r)L класс функций f, которая имеет абсолютно непрерывные производные до (r-1) порядка и у которой r-я производная принадлежит классу L.

Определение 3. Для непрерывной на [a,b] функции f (x) назовём модулем непрерывности первого порядка или же просто модулем непрерывности функцию f;, определённую на [0, b-a] при помощи следующего равенства:

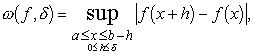(1.1)

или, что то же самое,

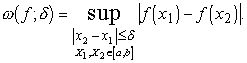(1.1’)

Свойства модуля непрерывности:



 есть функция, монотонно возрастающая;

 есть функция непрерывная;

 есть функция полуаддитивная в том смысле, что для любых и

(1.2)

Рекомендуем скачать другие рефераты по теме: аристотель реферат, международный реферат.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки