Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

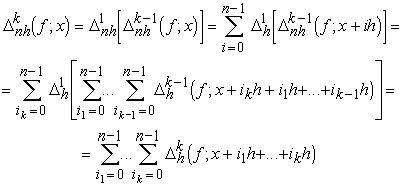
Лемма доказана.

Определение 5. Если измеримая периода (b-a) функция f(x)Lq (Lq-класс всех вещественных измеримых на [a,b] функции f(x)), то под её интегральным модулем гладкости порядка k1 понимают функцию

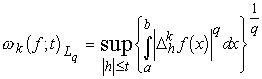
Лемма 3. Если то справедливо

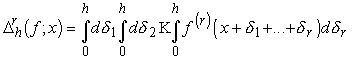(1.7)

Доказательство. В самом деле,

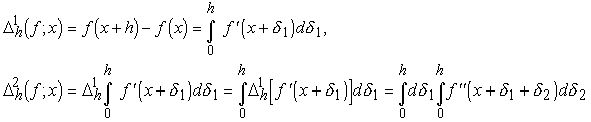
и так далее. Лемма доказана.

Определение 6. Если функция f(x) ограничена на [a,b], то под её модулем гладкости порядка k1 понимают функцию

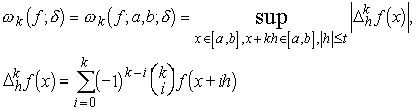
заданную для неотрицательных значений и в случае, когда k=1, представляющую собой модуль непрерывности.

Свойства модулей гладкости:

есть функция, монотонно возрастающая;

есть функция непрерывная;

При любом натуральном n имеет место ( точное) неравенство

(1.8)

а при любом -неравенство

(1.8’)

5) Если функция f(x) имеет всюду на [a,b] непрерывные производные до (r-1)-го порядка, и при этом (r-1)-я производная , то

(1.9)

Доказательство. 1) Свойство 1) немедленно вытекает из того, что

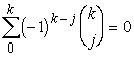
2) Свойство 2) доказывается точно так же, как и для случая обычного модуля непрерывности.

Рекомендуем скачать другие рефераты по теме: аристотель реферат, международный реферат.



Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки