Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Доказательство. Свойство 1) вытекает из определения модуля непрерывности.

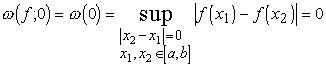
Свойство 2) вытекает из того, что при больших  нам приходится рассматривать sup на более широком множестве значений h. Свойство 4) следует из того, что если мы число представим в виде h=h1+h2, и , то получим

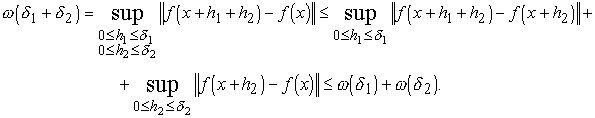
Из неравенства (1.2) вытекает, что если то т.е.

(1.3)

Теперь докажем свойство 3). Так как функция f (x) равномерно непрерывна на [a,b], то при и, следовательно, для любых ,

при

а это и означает, что функция  непрерывна.

Определение 4. Пусть функция f (x) определена на сегменте [a,b]. Тогда для любого натурального k и любых и h>0 таких, что k-й разностью функции f в точке x с шагом h называется величина

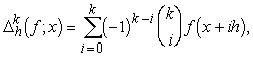(1.4)

а при и h>0 таких, что k-й симметричной разностью - величина

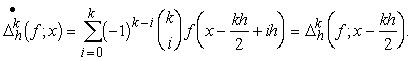(1.4’)

Лемма 1. При любых натуральных j и k справедливо равенство

(1.5)

Доказательство. Действительно, так как при любом натуральном k

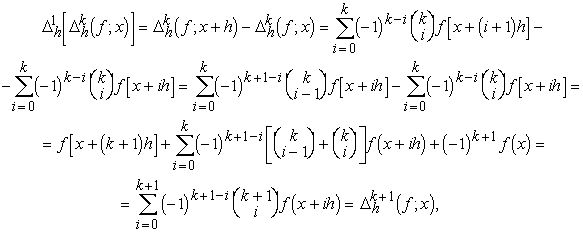
то

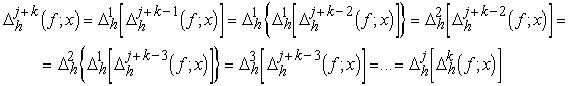
Лемма доказана.

Лемма 2. При любых натуральных k и n верна формула:

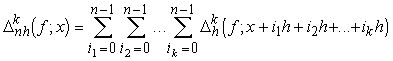(1.6)

Доказательство. Воспользуемся индукцией по k. При k=1 тождество (1.6) проверяется непосредственно:

.

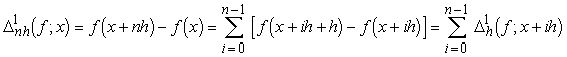Предполагая его справедливость при k-1 (k2), получим

Рекомендуем скачать другие рефераты по теме: аристотель реферат, международный реферат.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки