Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

l(x1) < l(x0) (5.8)

но линейная функция l(x) строго монотонно возрастает, так как

l(b) = f(b) > f(a) = l(a)

поэтому из (5.8) следует x1 < x0 , заменяя теперь отрезок [a, b] отрезком [x1, b] и замечая, что f(x1) < 0 , аналогично можно доказать, что x1 < x2 < x0, далее по индукции получим:

x1 < x2 < … < xn < … < x0,

Таким образом, последовательность {xn}, будучи монотонной, сходится. Пусть lim xn = c, при n®¥ . Переходя к пределу при n®¥ в равенстве (4.8) получим f(c)=0, т. е. последовательность {xn} сходится к корню уравнения (1.1).

Если | f ¢(x)|³m>0, a<x<b, то не трудно получить оценку погрешности сходимости последовательности {xn} через значения самой функции f(x) в точках xn. Действительно,

f(xn)= f(xn)- f(x0)= f ¢(xn)×(xn-x0),

xn<xn<x0, n = 1, 2, …,

Отсюда:

, n = 1, 2, …,

Остальные случаи, т. е. случаи:

 ,

 ,

 

рассматриваются аналогично разобранному (рис 2.8).

 

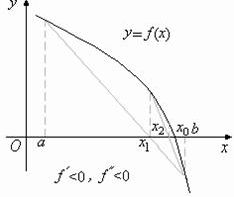
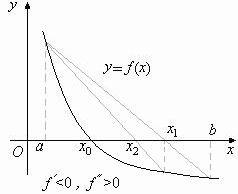
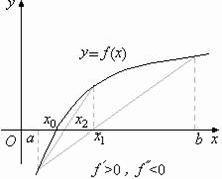
рис. 2.8

9. Усовершенствованный метод хорд

Если итерационная последовательность, полученная методом хорд, сходится, то скорость сходимости будет такой же, как и у метода итераций, - погрешность значения корня убывает, как геометрическая прогрессия. Существует усовершенствование способа хорд, дающее гораздо более быструю сходимость. В обычном методе хорд мы на каждом шагу используем один из концов отрезка [a, b] последнее получившееся приближение. Вместо этого можно использовать два последних приближения – ведь они ближе к искомому корню, чем концы отрезка [a, b].

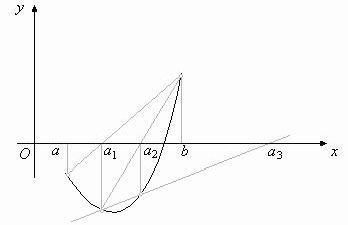
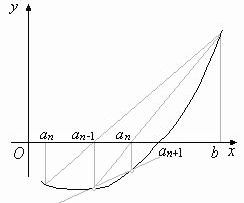 рис.1.9 а) б)   

Формула, при которой мы используем два последних приближения, имеет вид:

 (1.9)

При этом а1 вычисляется по формуле:

Рекомендуем скачать другие рефераты по теме: диплом вуза, стратегия реферат.



Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки