Предыдущая страница реферата | 20  21  22  23  24  25  26  27  28  29  30 | Следующая страница реферата

xÎ ( ; );

при а < 0 и D < 0

x = Æ (т. е. решении нет ).

Решение неравенства ax2 + bx + c < 0 сводится к решению рассмотренного неравенства, если обе части неравенства умножить на (-1).

Метод интервалов.

Пусть Рn(x) ¾ многочлен n-й степени с действительными коэффициентами, а c1, c2, ¼ , ci ¾ все действительные корни многочлена с кратностями k1, k2, ¼ , ki соответственно, причем с1 > c2 > ¼ > ci. Многочлен Pn(x) можно представить в виде

Рn(x) = (x - c1) k1(x - c2) k2 ¼ (x – ci)ki Qm(x),(3)

где многочлен Qm(x) действительных корней не имеет и либо положителен, либо отрицателен при всех хÎ R. Положим для определенности, что Qm(x) > 0. Тогда при х > c1 все сомножители в разложении (3) положительны и Рn(х) > 0. Если с1 ¾ корень нечетной кратности (k1 ¾ нечетное), то при хÎ (с2; с1) все сомножители в разложении (3), за исключением первого, положительны и Рn(х) 0 при хÎ (c2; с1). В этом случае говорят, что многочлен Рn(х) не меняет знак при переходе через корень с1.

Аналогичным способом, используя разложение (3), нетрудно убедится, что при переходе через корень с2 многочлен Рn(х) меняет знак, если k2 ¾ нечетное, и не меняет знака, если k2 ¾ четное. Рассмотренное свойство многочленов используется для решения неравенств методом интервалов. Для того чтобы найти все решения

Рn(х) > 0,(4)

достаточно знать все действительные корни многочлена Рn(х) их кратности и знак многочлена Рn(х) в произвольно выбранной точке, не совпадающей с корнем многочлена.

Пример: Решить неравенство

х4 + 3х3 – 4х > 0.(*)

Решение. Разложим на множители многочлен Р4(х), стоящий в левой части неравенства (*). Вынося множитель х за скобку, получаем

Р4(х) = х(х3 + 3х2 – 4).

Второй сомножитель, представляющий собой кубический многочлен, имеет корень х = 1. Следовательно, он может быть представлен в виде

х3 + 3х2 – 4 = (х-1)(х2 + 4х + 4) = (х-1)(х + 2) 2.

Таким образом, Р4(х) = х(х - 1)(х + 2) 2 и неравенство (*) может быть записано в виде

х(х –1)(х + 2)2 > 0. (**)

Решим неравенство (**) методом интервалов. При х > 1 все сомножители, стоящие в левой части неравенства, положительны.

Будем двигаться по оси Ох справа налево. При переходе через точку х = 1 многочлен Р4(х) меняет знак и принимает отрицательные значения, так как х = 1 ¾ простой корень (корень кратности 1); при переходе через точку х = 0 многочлен также меняет знак и принимает положительные значения, так как х = 0 ¾ также простой корень; при переходе через точку х = -2 многочлен знака не меняет, так как х = -2 ¾ корень кратности 2. Промежутки знакопостоянства многочлена Р4 (х) схематически представлены на рис 1. Используя этот рисунок, легко выписать множество решений исходного неравенства.

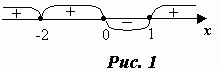
Ответ. х Î (-¥ ; -2) È (-2; 0) È (1; ¥ ).

Пример: Решить неравенство

(х2 – 3х – 2)(х2 – 3х + 1) < 10.

Решение: Пусть х2 – 3х – 2 = y. Тогда неравенство примет вид y(y +3) < 10, или y2 + 3y – 10 < 0, откуда (y + 5)(y – 2) < 0. Решением этого неравенства служит интервал –5 стоят знаки ½ х +1½ . Последнее в свою очередь, эквивалентно системе неравенств –(2х + 5) < х + 1 < 2х + 5,

откуда

Наименьшим целым числом х удовлетворяющей этой системе будет неравенств, является 0. Заметим, что х ¹ -1, иначе выражение в левой части данного неравенства не имеет смысла.

Ответ: 0.

Пример: Решить неравенство:

Решение: Пусть ½ х½ = y. Заметим далее, что ½ х½ + 1 > 0. Поэтому данное неравенство эквивалентно следующему: -2 ³ (y –2)(y + 1), или y2 – y £ 0, или 0 £ y£ 1, или 0 £ ½ х½ £ 1. Отсюда -1£ х £ 1.

Ответ: [-1; 1].

Пример: Решить неравенство

½ х2 – 3х + 2½ + ½ 2х + 1½ £ 5.

Решение. х2 – 3х + 2 отрицателен при 1 < x < 2 и неотрицателен при остальных х, 2х + 1 меняет знак при х = -Ѕ. Следовательно, нам надо рассмотреть четыре случая.

х < -Ѕ. В этом случае х2 – 3х + 2 > 0, 2х +1 < 0. Получаем неравенство х2 – 3х + 2 – 2х – 1 £ 5, х2 – 5х – 4 £ 0. Его решение £ х £ . С учетом условия х < -Ѕ находим £ х £ -Ѕ. – Ѕ £ х £ 1. Имеем неравенство х2 – х – 2 £ 0. Его решение –1 £ х £ 2. Следовательно, весь отрезок –Ѕ £ x £ 1удовлетворяет неравенству . 1 < x < 2. Получаем х2 – 5х + 6 ³ 0; х £ 2 или х ³ 3. Вновь подходит весь интервал. х ³ 2. Неравенство то же, что и в случае 2. Подходит лишь х = 2.

Ответ: £ х £ 2.

Пример: Решить неравенство.

½ ½ х3 + х - 3½ - 5½ £ х3 – х + 8.

Решение. Решим это неравенство не стандартным образом.

Неравенства с параметрами.

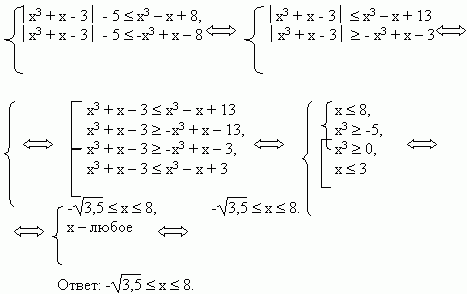
Неравенства с параметрами являются наиболее трудными задачами курса элементарной математики. Это объясняется тем, что их решения следует получать при всех допустимых значениях входящих в них параметров.

Пример: Для всех значений а решить неравенство

aх > 1/x.

Решение: Запишем неравенство в виде

тогда исходное неравенство эквивалентно двум системам неравенств:

ax2 – 1 > 0,ax2 – 1 < 0,

x > 0; x < 0.

Рассмотрим первую систему. Первое неравенство запишем в виде:

ax2 > 1.

Рекомендуем скачать другие рефераты по теме: первый снег сочинение, научный журнал.



Предыдущая страница реферата | 20  21  22  23  24  25  26  27  28  29  30 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки