Предыдущая страница реферата | 20  21  22  23  24  25  26  27  28  29  30 | Следующая страница реферата

При а > 0 оно эквивалентно неравенству х2 > 1/a, множество решений которого х < -1/  и x > 1/ . В этом случае решения первой системы: хÎ (1/ ; ¥ ). При а £ 0 левая часть неравенства ах2 –1 > 0 отрицательна при любом х и неравенство решений не имеет, а следовательно, не имеет решений и вся система неравенств.

Рассмотрим вторую систему. При а > 0 решениями неравенства ах2 – 1 0 и а £ 0 и для каждого из них построим графики функций, стоящих в левой и правой частях исходного неравенства. Заштрихованные промежутки оси Ох представляют собой решение неравенства в рассматриваемых случаях.

Графическая иллюстрация облегчает решение уравнений и неравенств с параметрами.

Ответ: Если а £ 0, то хÎ (-¥ ; 0); если а > 0, то хÎ (-1/ ; 0)È (1/ ; ¥ ).

Пример: Решить неравенство:

  

Решение: Преобразуем данное неравенство: 3m2х + 3 – 2mx2 – 6 < m + 9x; mx2 – 9x < m + 3; (m – 3)(m + 3)x < m + 3. Далее находим решение неравенства при различных значения параметра m:

Пусть (m – 3)(m + 3) > 0, т.е. m < -3 или m > 3. Тогда неравенство имеет решение х < 1/(m – 3). Пусть (m – 3)(m + 3) < 0, т.е. –3 < m < 3. Тогда неравенство имеет решение х > 1/(m – 3). Пусть (m – 3)(m + 3) = 0, т.е. m = 3 или m = -3. Тогда если m = 3, то неравенство примет вид 0× х < 6 и, значит выполняется при любом хÎ R. Если же m = -3, то неравенство примет вид 0× х < 0 и, следовательно, не имеет решении.

Пример: Для каждого неотрицательного значения параметра а решить неравенство

4а3х4 + 4а2х2 + 32х + а + 8 ³ 0.

Решение. Левая часть неравенства представляет собой многочлен как относительно х, так и относительно параметра а. Степени соответственно равны 4 и 3. Однако если умножить многочлен на а, а затем сделать замену y = ax, то в новом многочлене максимальная степень параметра а будет равна 2. Случай а = 0 дает нам ответ х ³ - ј. Будем теперь считать, что а > 0. Умножив обе части неравенства на а и сделав замену y = ax, получим

4y4 + 4ay2 + 32y + a2 + 8a ³ 0.

Левая часть представляет собой квадратный трехчлен относительно а:

a2 + (4y2 + 8)a + 4y2 + 32y ³ 0,

јD = (2y2 + 4) 2 – 4y2 – 32y = 16(y – 1) 2.

Раскладывая левую часть неравенства на множители, получим

(а + 2y2 + 4y)(a + 2y2 – 4y + 8) ³ 0,

или

(2y2 + 4y + a)(2y2 – 4y + 8 + a) ³ 0.

Второй множитель положителен при всех y, если а > 0. Приходим к неравенству 2y2 + 4y + a ³ 0, откуда, если 0

Ответ: Если а = 0, то х ³ - ј; если 0

Пример: Решить систему неравенств

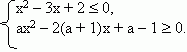
Решение: Поскольку решением первого неравенства является 1 £ х £ 2, то задача сводится (при а ¹ 0) к выяснению расположения корней квадратного трехчлена f(x) = ах2 – 2(а + 1)х + а –1 относительно отрезка [1; 2]. Имеем

јD = (а + 1) 2 – а(а – 1) = 3а + 1, f(1) = -3, f(2) = а – 5.

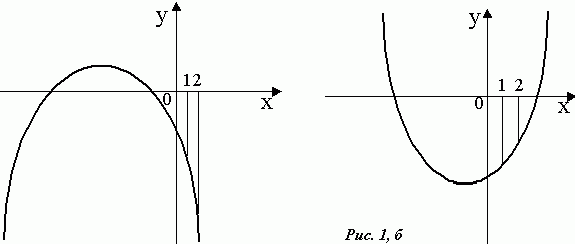
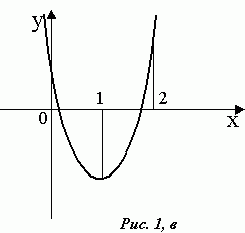
Область изменения параметра а оказалось разделенной на 4 части (не считая граничных точек).

Если а < - 1/3, второе неравенство, а следовательно и данная система не имеют решения. То же имеет место и при а = -1/3. Если –1/3 не имеет решения. То же имеет место и при а = 0.

Если 0 Ответ: Если а < 5, система не имеет решения; если а ³ 5, то 1/а(а + 1 + ) £ х £ 2.

Пример: Решить неравенство

½ 2х2 + х – а - 8½ £ х2 + 2х – 2а – 4.

Решить: Напомним, что неравенство ½ а½ £ b эквивалентно двойному неравенству –b £ a £ b. В нашем случае после преобразования приходим к системе неравенств

а £ -х2 + х + 4,

а £ х2 + х – 4.

Изобразим на плоскости (х; а) множество точек, координаты которых удовлетворяют полученной системе. При конкретном значении параметра а = a решением нашего неравенства будут абциссы тех точек горизонтальной прямой а = a , которые находятся в заштрихованной области. Найдем точки пересечения А(2; 2), В(-2; -2) наших точек парабол и вершину С(-0,5; -4,25) параболы а = х2 +х – 4.

Далее получаем: если а > 2, то соответствующая прямая пересекается с заштрихованной областью.

Если –2 (больший корень уравнения а = х2 + х – 4 или х2 – х – 4 + а= 0).

Если –4ј £ a £ -2, то горизонтальная прямая, соответствующая таким а, пересекается с заштрихованной областью по двум отрезкам. Решением неравенства будет

Системы рациональных неравенств.

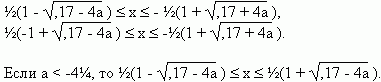
Пусть надо найти числовые значения х, при которых превращаются в верные числовые неравенства одновременно несколько рациональных неравенств. В таких случаях говорят, что надо решить систему рациональных неравенств с одним неизвестным х.

Чтобы решить систему рациональных неравенств, надо найти все решения каждого неравенства системы. Тогда общая часть всех найденных решений и будет решением системы.

Пример: Решить систему неравенств

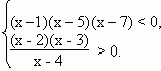
Сначала решаем неравенство

(х – 1)(х – 5)(х – 7) < 0.

Применяя метод интервала (рис. 1), находим, что множество всех решении неравенства (2) состоит из двух интервалов: (-¥ , 1) и (5, 7).

Теперь решим неравенство

Применяя метод интервалов (рис. 2), находим, что множество всех решении неравенства (3) также состоит их двух интервалов: (2, 3) и (4, +¥ ).

Теперь надо найти общую часть решении неравенств (2) и (3). Нарисуем координатную ось х и отметим на ней найденные решения. Теперь ясно, что общей частью решении неравенств (2) и (3) является интервал (5, 7) (рис. 3).

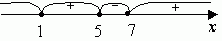
Следовательно, множество всех решении системы неравенств (1) составляет интервал (5, 7).

Пример: Решить систему неравенств

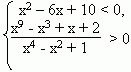
Рекомендуем скачать другие рефераты по теме: первый снег сочинение, научный журнал.



Предыдущая страница реферата | 20  21  22  23  24  25  26  27  28  29  30 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки