
Рациональные уравнения и неравенства
Категория реферата: Рефераты по математике
Теги реферата: сочинения по литературе, курсовая работа на тему право
Добавил(а) на сайт: Митькин.
Предыдущая страница реферата | 2 3 4 5 6 7 8 9 10 11 12 | Следующая страница реферата
уравнений: x3 = 1 или x3 = 4, т. е. X1 = 1 или X2 = 3Ö 4
Ответ: 1; 3Ö 4.
Пример 3.14. Решить уравнение (x3 – 27) / (x – 3) = 27
Решение. Разложим числитель на множители (по формуле разности кубов):
(x – 3)(x2 + 3x + 9) / (x – 3) = 27 . Отсюда:
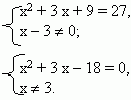
Квадратное уравнение x2 + 3 x – 18 = 0 имеет корни X1 = 3; X2 = -6
(X1 не входит в область допустимых значений).
Ответ: -6
Пример 3.15. Решить уравнение
(x2 + x –5) / x + (3x) / (x2 + x – 5) = 4.
Решение. Обозначим y= (x2 + x – 5) / x, тогда получаем уравнение y + 3 / y = 4.
Преобразуем его: y + 3 / y – 4 = 0, (y2 – 4y + 3) / y = 0, отсюда
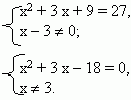
![]()
Квадратное уравнение y2 – 4y + 3 = 0 имеет корни Y1 = 1; Y2 = 3 (оба корня входят в область допустимых значений).
Таким образом корни, исходное уравнение эквивалентно (равносильно) совокупности уравнений
(x2 + x – 5) / x = 1 или (x2 + x – 5) / x = 3.
Преобразуем их:
(x2 + x – 5) / x – 1 = 0 или (x2 + x – 5) / x – 3 = 0;
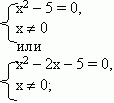
X1 = Ö 5; X2 = – Ö 5 или X3 = 1 + Ö 6; X4 = 1 – Ö 6
(все найденные корни уравнения входят в область допустимых значений).
Ответ: Ö 5; – Ö 5; 1 + Ö 6; 1 – Ö 6 .
Пример 3.16. Решить уравнение x(x + 2)(x + 3)(x + 5) = 72.
Рекомендуем скачать другие рефераты по теме: первый снег сочинение, научный журнал.
Предыдущая страница реферата | 2 3 4 5 6 7 8 9 10 11 12 | Следующая страница реферата