Предыдущая страница реферата | 6  7  8  9  10  11  12  13  14  15  16 | Следующая страница реферата



Примеры:

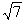– квадратическая иррациональность, так как 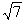является иррациональным корнем уравнения 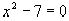. 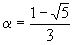– квадратическая иррациональность, так как представляет собой иррациональный корень уравнения 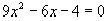. Здесь P=–1, Q=–3, D=5. 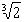не является квадратической иррациональностью.

Действительно, корень любого квадратного уравнения с целыми коэффициентами имеет вид 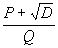, где P, Q, D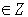, причем D>1. Если бы мы имели 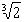=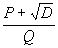, то, возводя это равенство в куб, мы получили бы, что 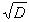– рациональное число, а следовательно, рациональным являлся бы и 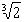, а это не так.

Теорема: Всякая периодическая непрерывная дробь изображает квадратическую иррациональность.

Доказательство: Пусть – смешанная периодическая цепная дробь, то есть 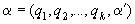, где 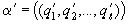– чисто периодическая цепная дробь.

Обозначим подходящие дроби к и 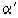соответственно через 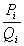и .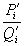

Так как 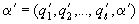, то, согласно формуле (5) из 1.1 этой главы, 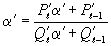. Выполнив необходимые преобразования, получаем: .

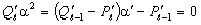Из этой формулы видно, что 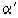удовлетворяет квадратному уравнению с целыми коэффициентами. Кроме того, 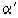- число иррациональное, так как оно представляет бесконечную непрерывную дробь. Таким образом, 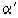- квадратическая иррациональность. Но по той же формуле 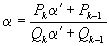, поэтому и является, очевидно, квадратической иррациональностью, что и требовалось доказать.

Докажем обратную теорему, которая носит имя Лагранжа.

Теорема Лагранжа: Всякая действительная квадратическая иррациональность изображается периодической непрерывной дробью.

Доказательство: Пусть – действительный иррациональный корень квадратного уравнения 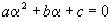(1) с целыми коэффициентами a, b, c.

При разложении в непрерывную дробь получаем 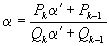(2), где 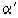– остаток порядка k+1.

Подставляя выражение из (2) в (1), получаем

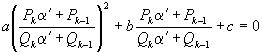
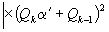
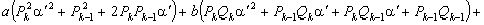
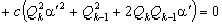
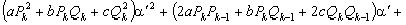
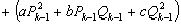
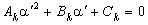(3), где

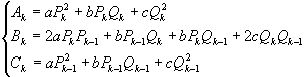(4)

Отсюда, во-первых, видно, что 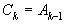(5), во-вторых, можно непосредственным вычислением установить, что 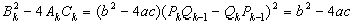(6).

Таким образом, дискриминант уравнения (3) такой же, как и дискриминант уравнения (1), откуда следует, что он от k не зависит.

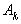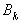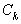Идея доказательства в дальнейшем заключается в том, чтобы показать, что при данном коэффициенты , , ограничены по модулю.

Если этот факт на самом деле имел бы место, то это означало бы, что коэффициенты, будучи целыми числами, могут принимать только конечное число различных значений. Вместе с тем и число возможных уравнений (3) было бы конечным, хотя k пробегает бесконечное множество значений. Но в таком случае и остатки 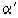(которые определяются из (3)), число которых бесконечно, могли бы принять только конечное число различных значений. Поэтому должны были бы существовать остатки 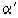с одинаковыми значениями, а это уже означает, что непрерывная дробь – периодическая.

Итак, докажем, что 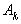, 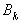и 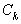ограничены по абсолютной величине. Достаточно сделать это для 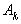, так как в силу соотношения (5), из ограниченности 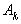уже как следствие вытекает ограниченность 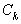, а в силу (6) – ограниченность .

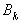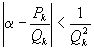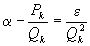Как известно из свойств подходящих дробей, или , где 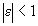, откуда .

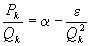Поэтому из первого равенства (4) имеем

Рекомендуем скачать другие рефераты по теме: таможенные рефераты, изложение по русскому языку 7.

Предыдущая страница реферата | 6  7  8  9  10  11  12  13  14  15  16 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки