Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Формулы сокращенного умножения

(a ± b)2 = a2 + 2ab + b2

a3 ± b3 = (a ± b)( a2ab+b2)

(a ± b)3 = a3 ± 3a2b + 3ab2 ± b3

a2 – b2 = (a + b)(a – b)

Свойства степени с целыми показателями

Формулы корней квадратного трехчлена ax2 + bx + c

Теорему Виета х1 и х2 — корни ax2 + bx + c в том и только том случае, если

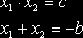
Разложение квадратного трехчлена ax2 + bx + c на множители.

Если х1, х2 — корни трехчлена, то ax2 + bx + c = а(х–х1)(х–х2)

Рассмотрим несколько примеров тождественных преобразований целых А.В.

Пример 1. Разложить многочлен на множители

Решение:

Задача заключается в том, чтобы сгруппировать слагаемые так, чтобы они имели общий множитель, который можно будет затем вынести за скобки, прейдя от суммы к произведению.

Итак.

Объединим крайние слагаемые в одну группу, а средние в другую:

2) Вынесем за скобки во второй группе общий множитель 2ab, получим:

3) Вынесем за скобки общий множитель первого и второго слагаемого (a2 + b2):

Рекомендуем скачать другие рефераты по теме: ответы по алгебре, реферат по обществознанию.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки