Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

Ответ: f(a,b,c) = 0 при b ¹ c, c ¹ a, a ¹ b.

4. Для успешного выполнения тождественных преобразований иррациональных выражений нужно помнить:

1. Определение арифметического корня n-ой степени:

Если  и n – натуральное число большее 1, то существует только одно неотрицательное число x такое, что выполняется равенство . Это число х называется арифметическим корнем n-ой степени из неотрицательного числа а и обозначается .

Пример.

Если n – нечетное натуральное число большее 1 и а < 0, то под  понимают такое отрицательное число х, что .

Пример.

2. Из определения 1. Следует, что если в алгебраическом выражении есть корни четной степени, то подкоренные выражения таких корней должны быть неотрицательными, что учитывается при определении области определения алгебраического выражения.

Пример.

Область определения выражения

3. Определение модуля числа.

Модулем числа а называется само число а, если  и противоположное ему число, если а < 0 т.е.

4. Свойства арифметического корня:

Если n, k, m – натуральные числа,  то:

1°

2° 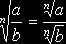 , если b ¹ 0.

Замечание. Если a < 0, b < 0, то свойства 1° и 2° принимают вид

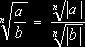
3°  

4°  

5°  

6°  

Рекомендуем скачать другие рефераты по теме: ответы по алгебре, реферат по обществознанию.



Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки