
Устойчивость систем дифференциальных уравнений
Категория реферата: Рефераты по математике
Теги реферата: курсовые работы, скачать сочинение
Добавил(а) на сайт: Глинин.
Предыдущая страница реферата | 4 5 6 7 8 9 10 11 12 13 14 | Следующая страница реферата
причем функция ![]() определена и
непрерывна в области вида
определена и
непрерывна в области вида ![]() . Условие (9) также выполняется. Действительно,
. Условие (9) также выполняется. Действительно, 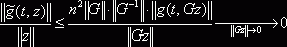 в силу (9), ограниченности
в силу (9), ограниченности ![]() и
и ![]() и поскольку
и поскольку ![]() эквивалентно
эквивалентно ![]() . При этом, как отмечалось, имеет место равномерность по t.
. При этом, как отмечалось, имеет место равномерность по t.
Согласно лемме
из п. 2.1. вопрос об устойчивости тривиального решения уравнения (8)
эквивалентен вопросу об устойчивости тривиального решения уравнения (13). Так
как ![]() , где
, где ![]() — собственные числа
матрицы
— собственные числа
матрицы ![]() , а
, а ![]() — мультипликаторы
линейного уравнения
— мультипликаторы
линейного уравнения ![]() , называемые также мультипликаторами периодического решения
, называемые также мультипликаторами периодического решения ![]() , то из теорем 5 и 6 вытекает следующая теорема:
, то из теорем 5 и 6 вытекает следующая теорема:
Теорема 8. Если модули всех мультипликаторов периодического решения периодического уравнения (1) меньше единицы, то это решение асимптотически устойчиво. Если же модуль хоть одного из мультипликаторов больше единицы, то оно неустойчиво.
Рассмотрим
смешанный случай, когда исследуется устойчивость -периодического решения ![]() автономного уравнения
(10). Дифференцируя тождество
автономного уравнения
(10). Дифференцируя тождество ![]() , получаем
, получаем ![]() . Следовательно, функция
. Следовательно, функция ![]() является -периодическим
решением уравнения в вариациях
является -периодическим
решением уравнения в вариациях ![]() . По следствию 1 п. 1.5. один из мультипликаторов равен
единице. Если среди остальных мультипликаторов имеются такие, модули которых
больше единицы, то решение
. По следствию 1 п. 1.5. один из мультипликаторов равен
единице. Если среди остальных мультипликаторов имеются такие, модули которых
больше единицы, то решение ![]() неустойчиво по теореме
8. В противном случае теорема 8 неприменима.
неустойчиво по теореме
8. В противном случае теорема 8 неприменима.
Теорема 9.
(Андронова-Витта) Если ![]() мультипликаторов
периодического решения уравнения (10) имеют модули, меньшие единицы, то это
решение устойчиво по Ляпунову.
мультипликаторов
периодического решения уравнения (10) имеют модули, меньшие единицы, то это
решение устойчиво по Ляпунову.
Замечание.
Уравнение (10) автономно, поэтому наряду с решением ![]() имеются и решения
имеются и решения ![]() ,
, ![]() , следовательно, решение
, следовательно, решение ![]() не может быть
асимптотически устойчивым.
не может быть
асимптотически устойчивым.
2.7. Экспоненциальная устойчивость.
Рассмотрим
уравнение (10), в котором ![]() . Обозначим через
. Обозначим через ![]() траекторию, проходящую
через точку
траекторию, проходящую
через точку ![]() при
при ![]() . Предположим, что нулевое решение (10) асимптотически
устойчиво, причем существуют число
. Предположим, что нулевое решение (10) асимптотически
устойчиво, причем существуют число ![]() и функция
и функция ![]() ,
, ![]() при
при ![]() такие, что
такие, что ![]() при
при ![]() . В этом случае существуют положительные числа
. В этом случае существуют положительные числа ![]() такие, что при
такие, что при ![]() справедливо
неравенство
справедливо
неравенство
![]() . (14)
. (14)
Если имеет место
оценка (14), то говорят, что нулевое решение экспоненциально асимптотически устойчиво.
Например, в условиях теоремы 5 нулевое решение уравнения (8) экспоненциально
асимптотически устойчиво. Более того, нулевое решение уравнения (8)
экспоненциально асимптотически устойчиво при более слабых, чем в теореме 5, ограничениях на нелинейность ![]() . Достаточно, чтобы левая часть (9) удовлетворяла неравенству
. Достаточно, чтобы левая часть (9) удовлетворяла неравенству
![]() , где
, где ![]() — собственные числа
матрицы A (их
вещественные части по условию отрицательны).
— собственные числа
матрицы A (их
вещественные части по условию отрицательны).
Для автономного уравнения (10) из экспоненциальной устойчивости следует асимптотическая устойчивость, и наоборот. Однако для неавтономных систем справедливо только первое утверждение.
Для неавтономной системы по формуле (14) вводится аналогичное понятие экспоненциальной устойчивости, однако асимптотическая устойчивость. Кроме того, справедлив следующая теорема.
Теорема. Для
того чтобы линейная система ![]() была экспоненциально
устойчивой, необходимо и достаточно, чтобы существовали две квадратичные формы
была экспоненциально
устойчивой, необходимо и достаточно, чтобы существовали две квадратичные формы ![]() и
и ![]() , обладающие следующими свойствами:
, обладающие следующими свойствами:
1. ![]() вещественная, симметричная и ограниченная;
вещественная, симметричная и ограниченная;
2. ![]() вещественная, симметричная и ограниченная;
вещественная, симметричная и ограниченная;
3. ![]() ;
;
4. ![]() (см. п. 3.1).
(см. п. 3.1).
3. Второй метод Ляпунова.
3.1. Основные определения.
Рассмотрим дифференциальное уравнение
![]() , (1)
, (1)
где ![]() . Предположим, что G — область единственности и
. Предположим, что G — область единственности и ![]() при всех
при всех ![]() , т. е. уравнение (1) имеет тривиальное решение
, т. е. уравнение (1) имеет тривиальное решение ![]() . Рассмотрим вопрос об устойчивости этого решения.
. Рассмотрим вопрос об устойчивости этого решения.
Сущность второго
метода Ляпунова заключается в исследовании поведения некоторой функции ![]() как функции t при замене x на произвольное решение уравнения
(1). В дальнейшем используем определения устойчивости и асимптотической
устойчивости, где
как функции t при замене x на произвольное решение уравнения
(1). В дальнейшем используем определения устойчивости и асимптотической
устойчивости, где ![]() .
.
Под функцией
Ляпунова будем понимать любую непрерывную функцию ![]() такую, что
такую, что ![]() при всех
при всех ![]() . На множестве функций Ляпунова
. На множестве функций Ляпунова ![]() задан линейный
оператор D, определяемый
формулой
задан линейный
оператор D, определяемый
формулой
![]() . (2)
. (2)
Рекомендуем скачать другие рефераты по теме: решебник по физике, работа реферат.
Предыдущая страница реферата | 4 5 6 7 8 9 10 11 12 13 14 | Следующая страница реферата