Предыдущая страница реферата | 4  5  6  7  8  9  10  11  12  13  14 | Следующая страница реферата

Соответствующая система двух уравнений имеет вид

.

В качестве функции Ляпунова возьмем полную энергию системы .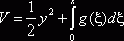

В силу условия  V —определенно-положительная функция, при этом

.

Следовательно, DV —отрицательная функция и множество M — интервал оси абсцисс при . Так как при  при , то множество M не содержит целых траекторий, отличных от положения равновесия .

По теореме 3 решение  системы асимптотически устойчиво, что и требовалось доказать.

Перейдем к рассмотрению неустойчивости. Пусть  — функция Ляпунова. Обозначим через  любую связную компоненту открытого множества  с началом координат на ее границе.

Теорема 4. Пусть существует функция Ляпунова  такая, что  не пусто и при . Тогда решение  уравнения (1) неустойчиво.

Доказательство. Пусть . Будем рассматривать решения  с начальной точкой . Достаточно показать, что для каждого из этих решений можно указать момент T (для каждого решения свой) такой, что .

Пусть это неверно, т. е. существует решение , удовлетворяющее при всех  неравенству . Покажем, что траектория решения  принадлежит  при . Действительно, по определению  она может покинуть область  только через ту часть ее границы, где . Но это невозможно, так как  и при возрастании  функция  строго возрастает, пока , в силу (3).

Итак, доказано, что при   и . Следовательно, по условию теоремы  при . Интегрируя (3) от  до , получаем

,

что противоречит ограниченности  при . Противоречие доказывает теорему.

Пример. Рассмотрим уравнение , где  — удовлетворяющая условию Липшица при  функция такая, что  при . Докажем неустойчивость решения .

Рассмотрим систему , соответствующую уравнению примера. В качестве функции Ляпунова возьмем . Имеем:

.

По теореме 4 решение  системы неустойчиво, что и требовалось доказать.

3.3. Устойчивость по первому приближению.

Рассмотрим дифференциальное уравнение

  ,          (8)

где  — заданная квадратичная форма.

Лемма 1. Если собственные числа матрицы A удовлетворяют условию

  ,         (9)

то уравнение (8) имеет единственное решение , являющееся квадратичной формой.

Рекомендуем скачать другие рефераты по теме: решебник по физике, работа реферат.



Предыдущая страница реферата | 4  5  6  7  8  9  10  11  12  13  14 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки