Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Необходимость. Пусть уравнение (3) устойчиво по Ляпунову. Тогда устойчиво его тривиальное решение, и выполняется (**). Пусть  фиксировано. Положим 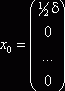. Если , то . Из (*) и (**) имеем , т. е.  ограничена. Аналогично доказывается ограниченность , а вместе с ними и матрицы .

2) Достаточность. Пусть  при . В силу (*)  при всех , что и дает асимптотическую устойчивость.

Необходимость. Пусть для любых  при . Положим 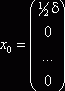. В силу (*) , следовательно, . Аналогично доказывается, что , , что означает  при . Теорема доказана.

Применим теорему 1 к исследованию устойчивости уравнения (3) с постоянной матрицей коэффициентов P. Уравнение (3) в этом случае имеет фундаментальную матрицу , , где  — жорданова форма матрицы P. По теореме 1, лемме 1 и следствию к ней устойчивость по Ляпунову, асимптотическая устойчивость и неустойчивость уравнения (3) эквивалентны соответственно ограниченности, бесконечной малости и неограниченности матрицы  при . Отсюда получаем следующую теорему:

Теорема 2. Линейная однородная система с постоянным коэффициентами: 1) устойчива по Ляпунову тогда и только тогда, когда среди собственных чисел матрицы коэффициентов нет таких, вещественные части которых положительны, а число мнимые и нулевые собственные числа либо простые, либо имеют только простые элементарные делители; 2) асимптотически устойчива тогда и только тогда, когда все собственные числа матрицы коэффициентов имеют отрицательные вещественные части.

Ниже рассматриваются необходимые и достаточные условия отрицательности корней характеристического уравнения линейной однородной системы с постоянными коэффициентами — критерий Гурвица (Рауса-Гурвица), а также частотный критерий Михайлова, являющийся геометрическим признаком, эквивалентным критерию Гурвица.

Определение. Полином , где , ,  называется полиномом Гурвица, если все его корни имеют отрицательные вещественные части.

Если полином  является полиномом Гурвица, то все .

Составим -матрицу Гурвица вида

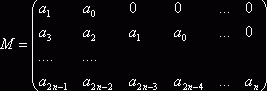
Теорема Гурвица (критерий Гурвица). Для того чтобы полином  являлся полиномом Гурвица, необходимо и достаточно, чтобы были положительны все главные диагональные миноры его матрицы Гурвица :

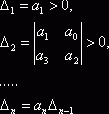
Если степень полинома  сравнительно большая, то применение критерия Гурвица становится затруднительным. В этом случае для определения расположения корней полинома  на комплексной плоскости иногда оказывается более удобным использование частотного критерия Михайлова.

Определение. Пусть , где , , . Кривая ,  называется годографом Михайлова функции .

Критерий Михайлова непосредственно следует из леммы:

Лемма 2. Угол поворота в положительном направлении ненулевого вектора  при  равен , где  — число корней полинома  с положительной вещественной частью с учетом их кратностей.

Критерий Михайлова. Для того чтобы полином , не имеющий чисто мнимых корней, являлся полиномом Гурвица, необходимо и достаточно, чтобы угол поворота в положительном направлении вектора  при  был бы равен .

Замечание. Если полином  есть полином Гурвица степени , то вектор  монотонно поворачивается в положительном направлении на угол , то есть годограф Михайлова, выходя из точки  положительной полуоси , последовательно пересекает полуоси , проходя  квадрантов.

2.3. Устойчивость периодических решений.

Рассмотрим уравнение (3) с периодическими коэффициентами, т. е. ,         (4)

где . По формуле (5) предыдущей главы уравнение (4) имеет в рассматриваемом случае фундаментальную матрицу , где  — неособая -периодическая непрерывная матрица, тем самым ограниченная вместе с обратной,  — жорданова матрица, собственные числа  которой — характеристические показатели уравнения (4). Из леммы 1 следует, что характеристические показатели играют при оценке фундаментальной матрицы ту же роль, что собственные числа , когда  постоянна. Учитывая, что , где  — мультипликаторы уравнения, получаем следующий результат:

Теорема 3. Линейная однородная система с периодическими коэффициентами: 1) устойчива по Ляпунову тогда и только тогда, когда все ее мультипликаторы не превышают по модулю единицы, а равные единице по модулю либо простые, либо им соответствуют простые элементарные делители матрицы монодромии; 2) асимптотически устойчива тогда и только тогда, когда модули всех мультипликаторов меньше единицы.

Пример. Рассмотрим уравнение из примера п. 1.5:

Уравнение будем называть устойчивым по Ляпунову, асимптотически устойчивым или неустойчивым, если таковой является соответствующая ему линейная система. Мультипликаторы находятся из уравнения : , где . Поэтому можно сделать вывод, что при  оба мультипликатора вещественны и один из них по абсолютной величине больше единицы, а при  мультипликаторы являются комплексно-сопряженными с модулями, равными единице. По теореме 3 при  уравнение  неустойчиво, а при  оно устойчиво по Ляпунову, но не асимптотически.

Рекомендуем скачать другие рефераты по теме: решебник по физике, работа реферат.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки