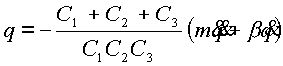Модель портального манипулятора
Категория реферата: Рефераты по науке и технике
Теги реферата: доклад на тему, педагогические рефераты
Добавил(а) на сайт: Кияк.
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 11 | Следующая страница реферата
В (2.4) для упрощения приняты следующие обозначения:
, 
, 
, 
, 
, 
.
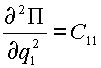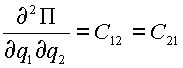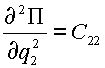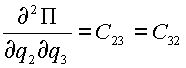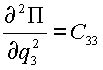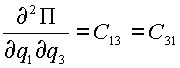Для составления дифференциальных уравнений свободных колебаний в форме уравнений Лагранжа второго рода, выразим потенциальную энергию через обобщенные координаты. Рассмотрим равновесие системы, на которую действуют силы 
…,
. Потенциальная энергия в состоянии устойчивого равновесия имеет минимум, равный нулю, а при вызванном действием сил 
отклонении от него выражается квадратичной формой вида (2.4).
Элементарная работа всех сил действующих на систему, по принципу возможных перемещений должна быть равна нулю:
|
|
(2.5) |
.Замечая, что
|
|
а также приравнивая к нулю коэффициенты при независимых вариациях 
, 
и 
, получаем три уравнения:
|
|
(2.6) |
,Здесь 
, 
и 
-
обобщенные силы для системы сил …,, уравновешивающих потенциальные силы, возникающие при отклонении системы из положения равновесия 
. Заменяя в (2.6) производные потенциальной энергии их выражениями согласно (2.4), получим систему уравнений, определяющих значение координат 
, 
и 
в положении равновесия:
|
|
(2.7) |
,причем 
, 
и 
.
Решение системы (2.7) имеет вид:
|
|
(2.8) |
,где
|
|
(2.9) |
.
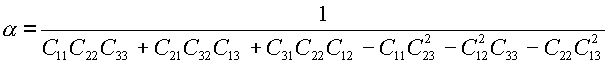На систему действуют обобщенные силы, которыми являются инерционные силы и силы сопротивления движению. Обычно в сложных системах в целях упрощения [4, 5] силу сопротивления принимают пропорциональной первой степени скорости движения. С целью упрощения условимся, что угол 
мал и координаты массы m можно записать как 
. Поэтому на основании кинетостатики можем записать:
|
|
(2.10) |
,где 
-
обобщенная сила, 
-
коэффициент сопротивления пропорциональный первой степени скорости движения массы m. Так как масса собственно консоли манипулятора МРЛ-901П меньше массы закрепленных на ней рабочих головок, захватов и деталей, для упрощения примем условие, что точка исследования колебаний (практически -
рабочий орган манипулятора) совпадает с точкой приложения сосредоточенной массы m.
Сила действует на все звенья манипулятора следовательно:
|
|
(2.11) |
Коэффициенты 
в (2.7) будем определять из того, что согласно (2.11) звенья можно рассматривать независимо друг от друга. Положим сначала, что действует только по координате , затем только по координате 
и наконец только по координате 
, тогда в выражение (2.7) можно переписать:
|
|
(2.12) |
,таким образом 
, используя (2.9) находим:
|
|
(2.13) |
Коэффициенты 
, 
и 
определяют податливость звеньев манипулятора по координатам , и соответственно. Выражая податливость звеньев через их жесткость, запишем:
|
|
(2.14) |
, где 
, 
и 
жесткости звеньев по координатам , и соответственно.
Подставляя (2.14) , (2.11) и (2.10) в (2.8) получим:
|
|
(2.15) |
Для решения этой системы нужно выразить скорость и ускорение массы m через их составляющие:
|
|
(2.16) |
.Поскольку в манипуляторе суммарную жесткость удобно экспериментально определять, прикладывая соответствующее усилие к его рабочему органу, и так как в конечном итоге необходимо определить положение массы m, координаты которой выражаются как , то для этого достаточно сложить уравнения в выражении (2.15):
|
|
(2.17) |
или:
|
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 11 | Следующая страница реферата Поделитесь этой записью или добавьте в закладкиКатегории: |
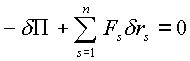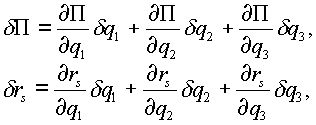
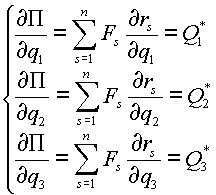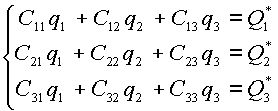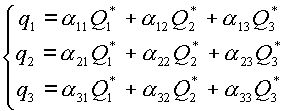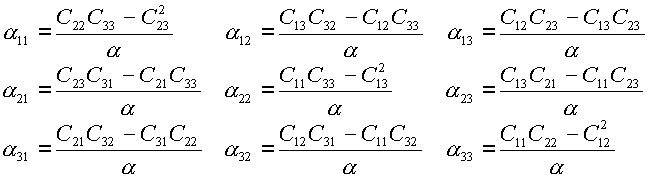
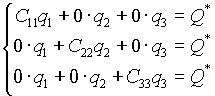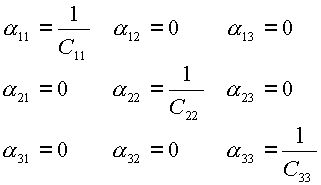
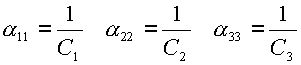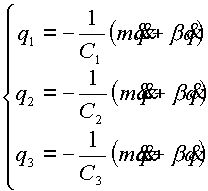
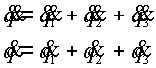