Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

Погрешность при замене А на Аn выражается суммой остатка аn=an+1+an+2+... Т.к. ряд сходится, то и поэтому при достаточно большом n погрешность станет сколь угодно малой. Другими словами, искомое А посредством частичной суммы Аn указанного ряда можно выразить с любой заданной точностью.

Если ряд знакочередующийся, удовлетворяет условиям признака Лейбница, то сумма остатка имеет знак своего первого члена и по модулю не превышает его.

В случае ряда с положительными членами 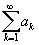необходимо найти новый ряд 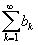с большими членами 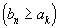, который бы легко суммировался, и в качестве оценки для суммы остатка 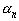взять сумму 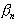остатка этого ряда.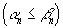

3.3. Ряды Фурье.

Мы показали приближение некоторых функций алгебраическими многочленами, теперь покажем, как приближаются функции тригонометрическими многочленами. Инструментом для этого будут ряды Фурье.

Тригонометрическим рядом называют функциональный ряд вида: 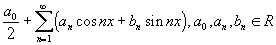называют коэффициентами ряда.

Пусть данный тригонометрический ряд сходится и его сумма равна f(x). Тогда .

Тригонометрической системой функций называют бесконечное множество функций 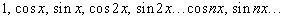Эта система обладает свойствами:

1.Определённый интеграл по отрезку 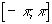от квадрата любой функции отличен от 0, причём

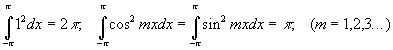
2. Определённый интеграл по отрезку 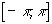от произведения любых двух различных функций равен нулю, т.е.

, ,

, ,

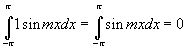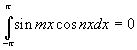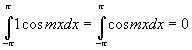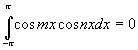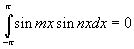
Замечание 1: Система функций 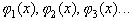называется ортогональной на отрезке [a,b], если

1.

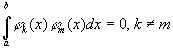
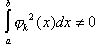
Видим, что тригонометрическая система функций является ортогональной на отрезке .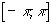

Будем считать, что выполнено условие, при котором этот тригонометрический ряд можно интегрировать почленно, тогда его коэффициенты определяются формулами:

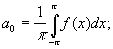
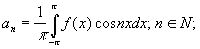
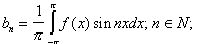
Тригонометрический ряд, определяемый такими коэффициентами, называется рядом Фурье, а числа an, bn- коэффициентами Фурье функции f(x).

Замечание 2: Формулы a0 и an можно объединить в одну: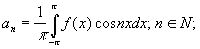

При этом появляется удобство обозначения начального члена тригонометрического ряда через a0/2, а не через a0. Замечание 3: Два аналитических выражения могут совпадать в некотором промежутке, но не совпадать при этом на всей числовой прямой.

Пример:

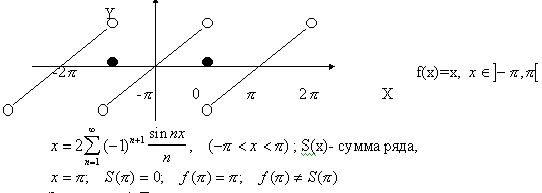
Замечание 4: Тригонометрическим рядом на всей числовой прямой можно представить только периодическую функцию.

Рекомендуем скачать другие рефераты по теме: поняття реферат, дипломная работа школа.



Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки