Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата



1.1. Основная теорема аппроксимации линейном нормированном пространстве

Пусть Е- произвольное нормированное пространство, пусть g1,g2...gn- n линейно- независимых элементов из Е. Основную задачу аппроксимации применительно к рассматриваемому нами “линейному случаю” можно сформулировать следующим образом: дан элемент х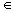Е, требуется определить числа 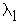,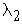... 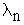так, чтобы величина 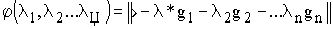получила наименьшее значение.

Докажем, что требуемые значения чисел 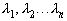существуют.

Предварительно заметим, что 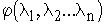- есть непрерывная функция своих аргументов. Действительно, в силу неравенства треугольника:

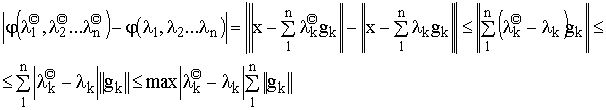
Введём теперь вторую непрерывную функцию:

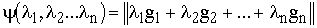
На “сфере” 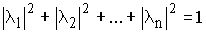, которая является ограниченным замкнутым множеством точек в n-мерном конечном Евклидовом пространстве, функция 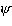по известной теореме Вейерштрасса имеет некоторый минимум .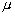

Неотрицательное число 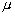не может равняться 0, так как векторы g1,g2...gn линейно независимы. Так же 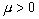. Обозначим 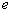(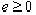)- нижняя грань значения функций 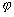. Если

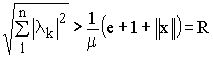, то

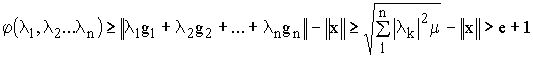
Желая найти минимум функции , мы можем ограничиться рассмотрением только значений 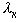, для которых 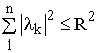, т.е. рассмотрением функции 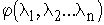в ограниченной замкнутой области, а в такой области непрерывная функция имеет минимум.

Итак, существование линейной комбинации 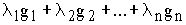, дающей наилучшую аппроксимацию элемента х, доказано.

Строго нормированное пространство.

Возникает вопрос, когда выражение 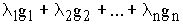, дающее наилучшую аппроксимацию элемента х, будет единственным для ?

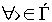Указанная единственность во всяком случае имеет место тогда, когда пространство Е строго нормировано, т.е. когда в неравенстве 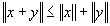, 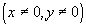знак “=” достигается только при ,.

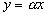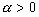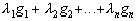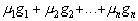В самом деле, допуская, что пространство Е строго нормировано, предположим, что элемент х имеет два выражения: и наилучшего приближения, причём g1,g2...gn линейно независимы.

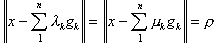где, как легко видеть, можно принять, что 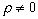и, поскольку 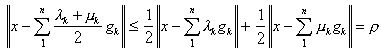, то

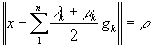, и, значит,

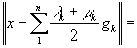
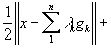
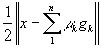
Следовательно, в силу строгой нормированности пространства: .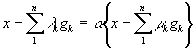

В этом соотношении 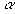должно =1, т.к. в противном случае элемент х был бы линейной комбинацией элементов g1,g2...gn и, значит, было бы 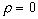. Но если =1, то

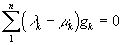и, значит, 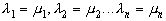, т.к. элементы g1,g2...gn линейно независимы. Таким образом, рассматриваемые выражения- тождественны.

Примером строго нормированного пространства является пространство Н, а также Lp при р>1, но пространства С и L не являются строго нормированными.

Действительно, возьмём интервал [-1,1] и две линейно независимые функции x(t) и y(t) 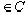, модули которых принимают свои максимальные значения в одной и той же точке 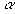интервала, причём arg x(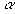)=arg y().

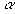Тогда очевидно, 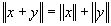. Чтобы доказать, что не есть строго нормированное пространство, достаточно взять x(t)=1, при 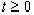и x(t)=0, при t<0 ,а y(t)=1-x(t).

Геометрическая интерпретация.

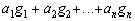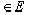Проблема, существование решения которой мы ранее доказали, допускает полезную геометрическую интерпретацию. Действительно, совокупность точек вида , где зафиксированные элементы g1,g2...gn линейно независимы, а a1,a2...anпробегают всевозможные комплексные числа, представляют некоторое линейное многообразие 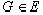в том смысле, что из 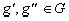следует, что 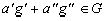при произвольных комплексных 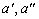. Это линейное многообразие, очевидно, является пространством, так как оно содержит точку 0. При n=1 мы получаем “прямую”; при n=2- “плоскость”, а вообще- “n- мерную плоскость”.

Рекомендуем скачать другие рефераты по теме: поняття реферат, дипломная работа школа.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки