Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Наша проблема, таким образом, состояла в нахождении точки конечномерного подпространства G пространства E, которая от заданной точки х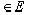 находится на кратчайшем расстоянии (в метрике пространства Е). Мы доказали, что такая точка в G существует.

Если само пространство Е не является конечномерным, т.е. если в нём имеется сколько угодно линейно независимых между собой векторов, то Е содержит бесконечномерные подпространства. Пусть G- такое подпространство.

Возникает вопрос, существует ли в G точка, наименее удалённая от заданной точки 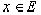. Заметим, если пространство Е строго нормировано, то в G во всяком случае не может существовать более одной точки, наименее удалённой от данной точки .

1.2. Теоремы аппроксимации в пространстве Н.

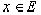Пусть G- некоторое подпространство пространства Гильберта Н, и пусть точка x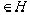- точка, не принадлежит G. Если в G существует точка y, наименее удалённая от x, то вектор x-y ортогонален к каждому вектору g из G, т.е. (x-y, g)=0, 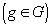. Чтобы доказать это утверждение, предположим, что в G существует вектор f, для которого 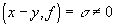, и рассмотрим вектор .

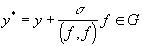Имеем 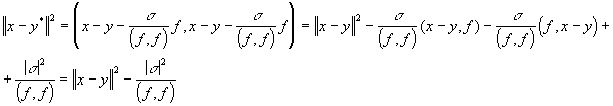и, значит: 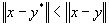, а это противоречит предположению, что y- есть наименее удалённая точка от x подпространства G. Вектор y из G, обладающий тем свойством, что разность x-y ортогональна к G, естественно назвать проекцией x на G.

В этом случае, когда подпространство конечномерно и образовано линейно независимыми векторами g1,g2...gn, мы можем, пользуясь доказанными предложениями, фактически найти вектор y=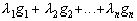, наименее уклоняющийся от вектора x. Действительно, вектор y- есть проекция x на G и, значит, он должен удовлетворять уравнениям:

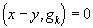(k=1,2...n) (1), которые в подробной записи имеют вид:

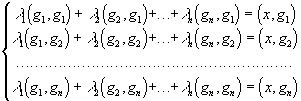(2)

и представляют систему линейных уравнений, для нахождения коэффициентов .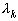

Детерминант этой системы, т.е.

,

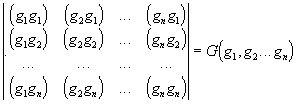носит название детерминанта Грама системы векторов g1,g2...gn.

Так как пространство Н строго нормировано, а векторы gi линейно независимы, то при любом векторе x система (2) имеет одно и только одно решение. Отсюда вытекает, что детерминант Грама линейно независимых векторов всегда отличен от нуля.

Найдём ещё выражение для квадрата погрешности, с которой вектор y аппроксимирует вектор x, т.е. для величины .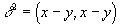

В силу (1), имеем равенство

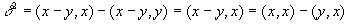или

.

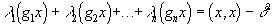Присоединяя это уравнение к системе (2) и исключая 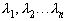, найдём, что

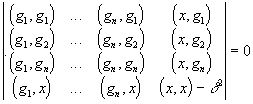, откуда .

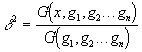Итак, мы нашли: 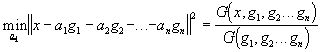(3)

Из этого соотношения, и из того, что G(g1)=(g1,g1)>0 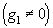вытекает, что детерминант Грама всегда больше либо равен нулю, причём он обращается в нуль тогда и только тогда, если между векторами есть линейная зависимость (в частности, если один из векторов равен нулю).

1.3. Первая теорема Вейерштрасса.

Мы рассмотрели теорему аппроксимации в произвольном линейном нормированным пространстве Е. Теперь рассмотрим пример линейного нормированного пространства- пространство С.

Пространство С: совокупность всех непрерывных функций x=x(P) от точки Р в ограниченном замкнутом множестве 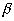обычного пространства любого числа измерений- это есть линейное нормированное пространство.

Из теоремы в применении к пространству вытекает следующий факт: пусть f(x)- непрерывная функция в конечном интервале [a,b]; тогда при любом n существует полином 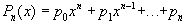, который среди полиномов n-й степени наименее уклоняется от f(x), в том смысле, что 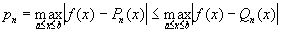, где Qn(x)- произвольный полином n-й степени. Ясно, что .

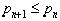Теперь докажем, что 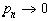при 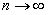. Это утверждение и составляет содержание теоремы Вейерштрасса (1885), которая гласит:

Рекомендуем скачать другие рефераты по теме: поняття реферат, дипломная работа школа.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки