Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата



Формула Тейлора для функций sinx, cosx, ex

Выведем формулы Тейлора для элементарных функций f(x)=sinx, f(x)=cosx, f(x)=ex.

Рассмотрим функцию f(x)=sinx. Найдём производную n+1- го порядка.

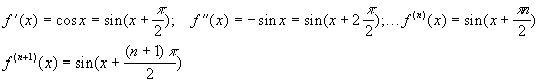
Вычислим значение функции и её производной при х=0.

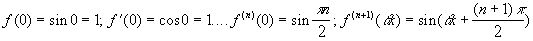
Подставим эти значения в формулу Тейлора:

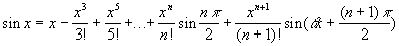
2.Аналогично находим формулу Тейлора для f(x)=cosx.

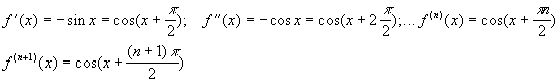
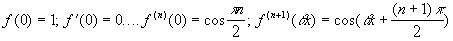
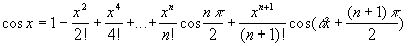
3.Рассмотрим функцию f(x)=ex.

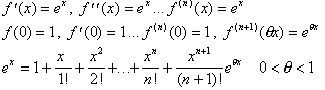
4.Рассмотрим функцию f(x)=(a+x)n ,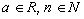

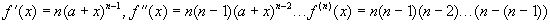
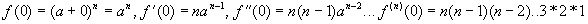
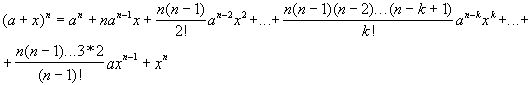
Эту формулу называют биномом Ньютона. Отметим частные случаи:

n=2 (a+x)2=a2+2ax+x2

n=3 (a+x)3=a3+3a2x+3ax2+x3

Приближение функций sinx, cosx, ex алгебраическими многочленами.

В формуле Тейлора для sinx положим n=2m-1

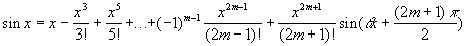
Остаточный член этой формулы имеет вид:

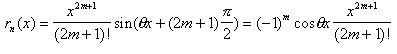
Оценим его модуль. Поскольку

Рекомендуем скачать другие рефераты по теме: поняття реферат, дипломная работа школа.



Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки