Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

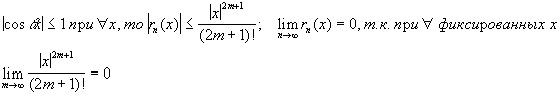
Отбрасывая остаточный член, получим приближённо:

.

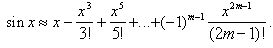Она может быть применена для вычисления значений функции f(x)=sinx при заданных значениях аргумента х. Эти вычисления сводятся к вычислениям значений алгебраического многочлена степени 2m-1 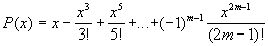. Следовательно, вместо функции f(x)=sinx можно рассматривать алгебраический многочлен, который приближённо заменяет её. Говорят, что указанный многочлен приближает данную функцию. Оценка такого приближения определяется формулой: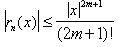

Полагая n=2m в формуле для cosx, аналогично: 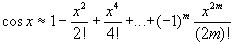, погрешность .

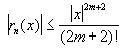Например, для приближённой формулы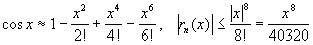

В случае функции f(x)=ex, получаем: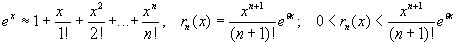

В общем случае, отбросив остаточный член, получим приближённую формулу:.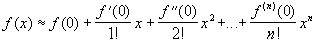

Она позволяет заменить данную функцию алгебраическим многочленом n-й степени:

Ряд Тейлора.

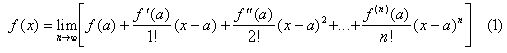
Обратимся к формуле (1). Разность между функцией f(x) и её многочленом в правой части называют отклонением, которое выражается остаточным членом rn(x).Если в формуле рассматривать всё больше и больше членов, то может оказаться, что отклонение стремится к нулю, но не для всякой функции и не для любого значения х. Однако существует широкий класс функций, для которых остаточный член действительно стремится к нулю при 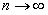, по крайней мере для значений, заполняющих некоторый промежуток, содержащий т.а. Именно для таких функций формула Тейлора позволяет вычислить f(x) с любой степенью точности. Если 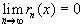, то из формулы Тейлора следует: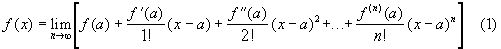

Число слагаемых является неограниченным. Выражение в правой части формулы называют рядом Тейлора, а функцию f(x)- суммой этого ряда.

Ряд Тейлора можно записать в таком виде:

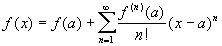, при а=0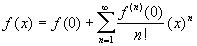

Выражение в правой части этой формулы называют рядом Маклорена. Получаем:

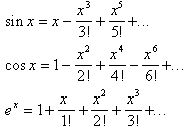
Условие сходимости:

Для разложения f(x) в степенной ряд (т.е. в ряд Тейлора), необходимо и достаточно, чтобы предел остаточного члена формулы Тейлора был равен нулю: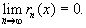

Степенной ряд сходится при любых х или говорят, что его областью сходимости является промежуток 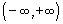. Из этих формул видно, что sin(-x)=-sinx, т.е. f(x)=sinx- нечётная функция.

cos(-x)=cosx, f(x)=cosx- чётная функция.

Примеры разложения функций в степенные ряды.

Степенной ряд 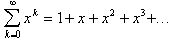можно рассматривать как геометрический с первым членом а=1 и знаменателем q=x. Если 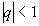, т.е. 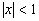, то данный ряд сходится. .

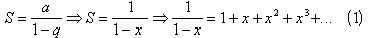Мы получили разложение функции 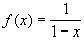в степенной ряд. Этот ряд сходится при .

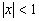Аналогичными рассуждениями можно установить, что 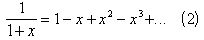сходится при . Степенной ряд можно почленно дифференцировать и интегрировать, т.е. обращаться с ним как с многочленом.

В формуле (1) заменим x на t и проинтегрируем получившийся ряд на промежутке [0,x]; ,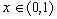

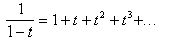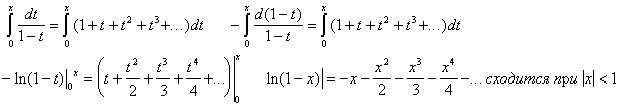
Рекомендуем скачать другие рефераты по теме: поняття реферат, дипломная работа школа.



Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки