
Математические модели в естествознании
Категория реферата: Рефераты по математике
Теги реферата: договор реферат, инновационная деятельность
Добавил(а) на сайт: Добромила.
Предыдущая страница реферата | 6 7 8 9 10 11 12 13 14 15 16
Возможны четыре случая соотношений относительных приспособленностий генотипов:
1. 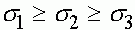 ,
,
2. 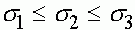 ,
,
3. 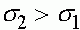 ,
, 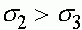 ,
,
4. 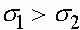 ,
, 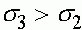 .
.
Первый случай. Следует предполагать, что одно из неравенств строгое, в противном случае нет отбора. Поскольку либо 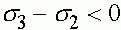 , либо
, либо 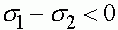 , то отсутствует внутреннее равновесное состояние
, то отсутствует внутреннее равновесное состояние 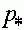 и
и 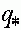 для частот аллелей, заданных формулами (18) и (19). Действительно, одно из этих чисел будет отрицательным. В силу проведенных выше рассуждений все траектории отображения
для частот аллелей, заданных формулами (18) и (19). Действительно, одно из этих чисел будет отрицательным. В силу проведенных выше рассуждений все траектории отображения 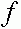 стремятся к одному из крайних равновесных состояний: либо
стремятся к одному из крайних равновесных состояний: либо 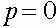 , либо
, либо 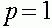 . Разность
. Разность 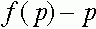 не обращается в ноль, а, следовательно, не меняет знак на интервале
не обращается в ноль, а, следовательно, не меняет знак на интервале 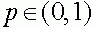 . Если она положительна, то траектории стремятся к состоянию равновесия
. Если она положительна, то траектории стремятся к состоянию равновесия 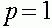 . В противном случае траектории стремятся к нулевому состоянию равновесия. Знак разности можно определить, анализируя ее в малых окрестностях состояний равновесия. Пусть для определенности
. В противном случае траектории стремятся к нулевому состоянию равновесия. Знак разности можно определить, анализируя ее в малых окрестностях состояний равновесия. Пусть для определенности 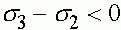 . Тогда из формулы Тейлора и (22) следует, что
. Тогда из формулы Тейлора и (22) следует, что
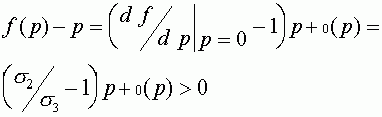
для 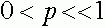 . Совершенно аналогично проверяется, что для случая
. Совершенно аналогично проверяется, что для случая 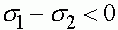 данная разность положительна при
данная разность положительна при 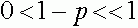 .
.
Таким образом, все траектории отображения стремятся к состоянию равновесия 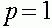 . Происходит вытеснение менее приспособленного аллеля a из популяции. Однако этот процесс протекает очень медленно. Пусть, например,
. Происходит вытеснение менее приспособленного аллеля a из популяции. Однако этот процесс протекает очень медленно. Пусть, например, 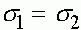 и
и 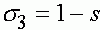 , где
, где 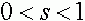 . Тогда можно показать, что
. Тогда можно показать, что 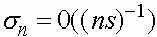 , при
, при  .
.
Второй случай полностью симметричен первому. Происходит медленное вытеснение аллеля A.
Третий случай. Выполнено условие (21), при котором существует внутреннее состояние равновесия 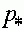 , определенное формулой (18). Выясним, какие знаки имеет разность
, определенное формулой (18). Выясним, какие знаки имеет разность 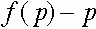 на интервалах
на интервалах 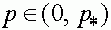 и
и 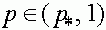 . Для
. Для 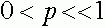 как и в первом случае имеем
как и в первом случае имеем
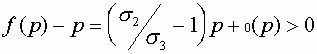 ,
,
следовательно 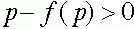 для всех
для всех 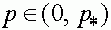 . Траектория с начальным условием
. Траектория с начальным условием 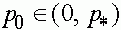 стремится к состоянию равновесия
стремится к состоянию равновесия 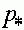 . Состояние равновесия
. Состояние равновесия 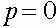 неустойчиво.
неустойчиво.
В свою очередь для значений 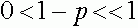 по формуле Тейлора получаем:
по формуле Тейлора получаем:
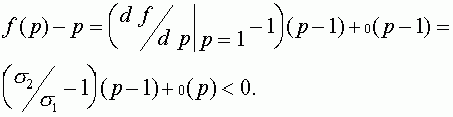
Для всех 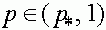 выполнено неравенство
выполнено неравенство 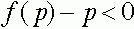 . Траектории с начальным условием
. Траектории с начальным условием 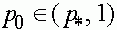 также стремятся к внутреннему состоянию равновесия
также стремятся к внутреннему состоянию равновесия 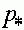 , а состояние равновесия
, а состояние равновесия 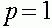 неустойчиво.
неустойчиво.
Итак, в рассматриваемом случае независимо от начальных условий все траектории стремятся к устойчивому состоянию равновесия:
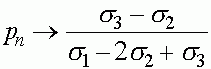 ,
, 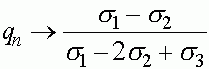 .
.
Популяция эволюционизирует к этому состоянию. В ней присутствуют все генотипы AA, Aa, aa, включая менее приспособленные. Как уже отмечалось, такое состояние называется балансированным полиморфизмом.
Четвертый случай. Здесь также существует внутреннее состояние равновесия 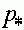 . Однако, знаки функции
. Однако, знаки функции 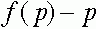
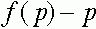 на интервалах
на интервалах 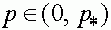 и
и 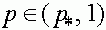 будут противоположными тем, которые имели место в третьем случае:
будут противоположными тем, которые имели место в третьем случае: 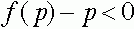 для
для 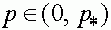 и
и 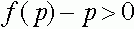 для
для 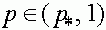 . Вследствие этого, для траекторий с начальными условиями
. Вследствие этого, для траекторий с начальными условиями 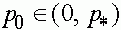 получаем
получаем 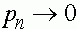 при
при  (соответственно
(соответственно 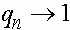 ). Аллель A вытесняется из популяции. Если же
). Аллель A вытесняется из популяции. Если же 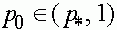 , то
, то 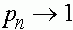 и
и 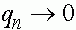 при
при  . Постепенно вытесняется из популяции аллель a. Какой аллель теряется - зависит от начального состояния популяции. Равновесный полиморфизм оказывается неустойчивым.
. Постепенно вытесняется из популяции аллель a. Какой аллель теряется - зависит от начального состояния популяции. Равновесный полиморфизм оказывается неустойчивым.
Поведение траектории 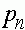 можно изобразить в виде фазовой диаграммы, где вдоль оси абсцисс откладывается значение
можно изобразить в виде фазовой диаграммы, где вдоль оси абсцисс откладывается значение 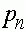 , а вдоль оси ординат - величина
, а вдоль оси ординат - величина 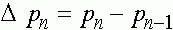 .
.
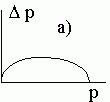
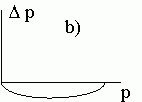
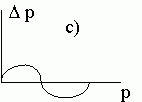
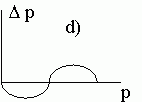
Диаграммы a), b), c), d) соответствуют случаям 1- 4.
Полную версию лекций см. ниже в заархивированных вариантах.
Скачали данный реферат: Kutlyev, Овчинников, Nenashev, Лыков, Lebedev, Avdoshkin.
Последние просмотренные рефераты на тему: шпоры по истории, работа реферат, республика реферат, бесплатные рефераты и курсовые.
Предыдущая страница реферата | 6 7 8 9 10 11 12 13 14 15 16