Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

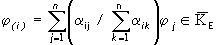, i=1,...,N,(7)

причем для изображения (5) цвета j (i), i=1,.…..,N, считаются попарно различными, а функции g(i), i=1,.…..,N, - удовлетворяющими условиям 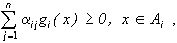i=1,.…..,N.

Нетрудно заметить, что в выражениях (5),(6) и (7) без потери общности можно принять условие нормировки 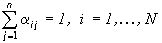, позволяющее упростить выражения (6) и (7) для распределений яркости и цвета. С учетом нормировки распределение яркости на Ai задается функцией 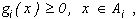а цвет на Ai равен

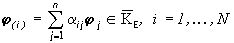(7*)

Форму изображения (5) определим как класс всех изображений

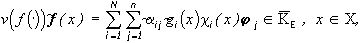(8)

,

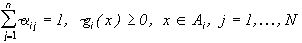каждое из которых, как и изображение (5), имеет постоянный цвет в пределах каждого Ai, i=1,...,N. Форма таких изображений не сложнее, чем форма f() (5), поскольку в изображении 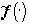на некоторых различных подмножествах Ai, i=1,...,N, могут совпадать значения цвета, которые непременрно различны в изображении f() (5). Совпадение цвета 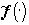на различных подмножествах Ai, i=1,...,N ведет к упрощению формы изображения 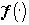по сравнению с формой f() (5). Все изображения 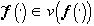, имеющие различный цвет на различных Ai, i=1,...,N,считаются изоморфными fи между собой), форма остальных не сложнее, чем форма f. Если 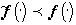, то, очевидно, .

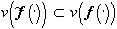Если в (8) яркость 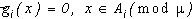, то цвет 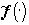на Ai считается произвольным (постоянным), если же 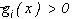в точках некоторого подмножества 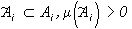, то цвет 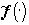на Ai считается равным цвету 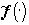на 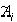, i=1,...,N.

Цвет изображения (8) может не совпадать с цветом (5). Если же по условию задачи все изображения 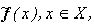, форма которых не сложнее, чем форма 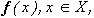, должны иметь на Ai, i=1,...,N, тот же цвет, что и у 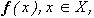то следует потребовать, чтобы 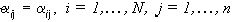, в то время, как яркости 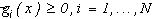остаются произвольными (если 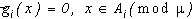, то цвет 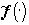на Ai определяется равным цвету f на Ai, i=1,...,N).

Нетрудно определить форму любого, не обязательно мозаичного, изображения fв том случае, когда допустимы произвольные изменения яркости 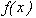при неизменном цвете j (x) в каждой точке 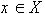. Множество, содержащее все такие изображения

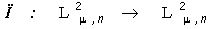(9)

назовем формой в широком смысле изображения , у которого f(x)¹ 0, m -почти для всех 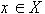, [ср. 2]. 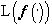является линейным подпространством 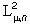, содержащем любую форму

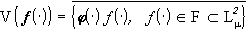,(10)

в которой включение 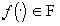определяет допустимые значения яркости. В частности, если 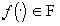означает, что яркость неотрицательна: 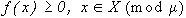, то 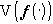- выпуклый замкнутый конус в 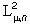, принадлежащий .

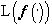Более удобное описание формы изображения может быть получено на основе методов аппроксимации цветных изображений, в которых форма определяется как оператор наилучшего приближения. В следующем параграфе дано представление формы изображения в виде оператора наилучшего приближения.

5. Задачи аппроксимации цветных изображений. Форма как оператор наилучшего приближения.

Рассмотрим вначале задачи приближения кусочно-постоянными (мозаичными) изображениями. Решение этих задач позволит построить форму изображения 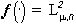в том случае, когда считается, что 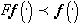для любого преобразования 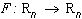, действующего на изображение 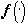как на вектор 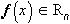в каждой точке 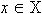и оставляющего 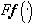элементом 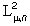, т.е. изображением. Форма в широком смысле 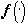определяется как оператор 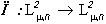наилучшего приближения изображения 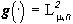изображениями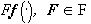

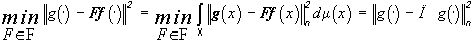
где 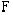- класс преобразований 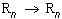, такой, что 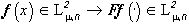. Иначе можно считать, что

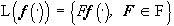(10*)

а 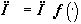- оператор наилучшего приближения элементами множества 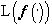, форма которых не сложнее, чем форма 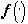. Характеристическим для 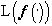является тот факт, что, если f(x)=f(y), то для любого.

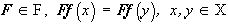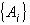5.1. Приближение цветного изображения изображениями, цвет и яркость которых постоянны на подмножествах разбиения поля зрения X.

Задано разбиение 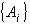, требуется определить яркость и цвет наилучшего приближения на каждом 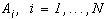. Рассмотрим задачу наилучшего приближения в 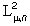цветного изображения f(× ) (2) изображениями (4), в которых считается заданным разбиение 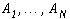поля зрения X и требуется определить 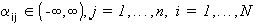из условия

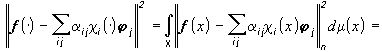
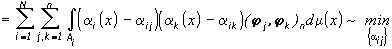(11)

Теорема 1. Пусть 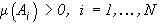. Тогда решение задачи (11) имеет вид

Рекомендуем скачать другие рефераты по теме: оформление доклада титульный лист, понятие культуры.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки