Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

Замечание 2. Если данные задачи доступны лишь в черно-белом варианте, то есть заданы числа 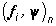, i=1,...,q, которые можно считать упорядоченными согласно условию 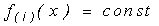, то, как показано в [3], искомое разбиение X состоит из множеств

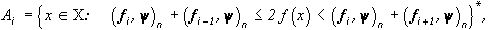
где 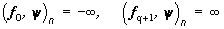, и имеет мало общего с разбиением (14).

Замечание 3. Выберем векторы fi, i=1,..,q единичной длины: 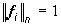, i=1,...,q. Тогда

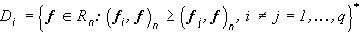.(16)

Множества (16) являются конусами в Rn , ограниченными гиперплоскостями, проходящими через начало координат. Отсюда следует, что соответствующее приближение 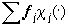изображения f инвариантно относительно произвольного преобразования последнего, не изменяющего его цвет (например 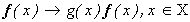), в частности, относительно образования теней на f.

Замечание 4. Для любого заданного набора попарно различных векторов 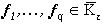оператор F, приведенный в теореме 2, определяет форму изображения, принимающего значения 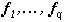соответственно на измеримых множествах 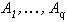(любого) разбиения X. Всякое такое изображение является неподвижной (в 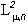) точкой F: 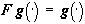, если 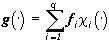, все они изоморфны между собой. Если некоторые множества из 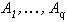- пустые, или нулевой меры, соответствующие изображения имеют более простую форму.

Иначе говоря, в данном случае формой изображения 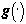является множество всех изображений, принимающих заданные значения 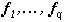на множествах положительной меры 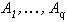любого разбиения X, и их пределов в .

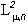Теоремы 1 и 2 позволяют записать необходимые и достаточные условия наилучшего приближения изображения f(× ) изображениями 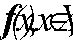, в котором требуется определить как векторы 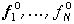, так и множества 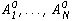так, чтобы

.

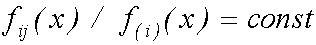Следствие 1.

Пусть Di ,i=1,...,N, - подмножества Rn (15), П - ортогональный проектор (13), 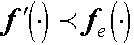, где 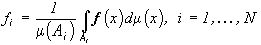. Тогда необходимые и достаточные условия 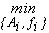суть следующи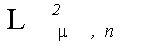е: , где , .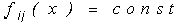

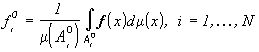Следующая рекуррентная процедура, полезная для уточнения приближений, получаемых в теоремах 1,2, в некоторых случаях позволяет решать названную задачу. Пусть 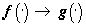- исходные векторы в задаче (14*), 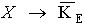- соответствующее оптимальное разбиение (14), F(1)- оператор наилучшего приближения и 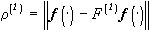- невязка. Воспользовавшись теоремой 1, определим для найденного разбиения 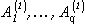оптимальные векторы 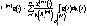. Согласно выражению (13) 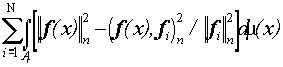, и соответствующий оператор наилучшего приближения (1) (13) обеспечит не менее точное приближение f(× ), чем F(1): 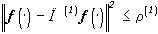. Выберем теперь в теореме 2 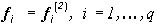, определим соответствующее оптимальное разбиение 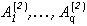и построим оператор наилучшего приближения F(2). Тогда . На следующем шаге по разбиению 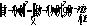строим 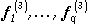и оператор (3) и т.д.

В заключение этого пункта вернемся к вопросу о построении исчерпывающего 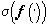-измеримого разбиения X, отвечающего заданной функции 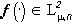. Выберем произвольно попарно различные векторы 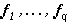из f(X) и построим по формуле (15) разбиение Rn 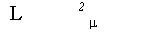. Для каждого q=1,2,... образуем разбиение E(N(q)), множества 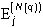, j=1,...,N(q), которого образованы всеми попарно различными пересечениями 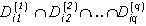множеств из 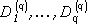. Последовательность соответствующих разбиений X 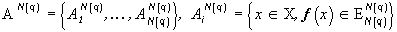, i=1,...,N(q), q=1,2... 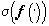-измеримы и 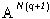является продолжением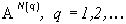

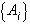5.2. Приближение изображениями, цвет которых постоянен на подмножествах разбиения поля зрения X.

Задано разбиение 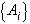, требуется определить цвет и распределение яркостей наилучшего приближения на каждом Ai,i=1,...,N.

Для практики, как уже было отмечено, большой интерес представляет класс изображений (5), цвет которых не изменяется в пределах некоторых подмножеств поля зрения, и задачи аппроксимации произвольных изображений изображениями такого класса.

Запишем изображение (5) в виде

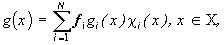(17)

где .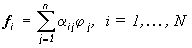

Пусть A1,...,AN - заданное разбиение X, 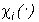- индикаторная функция Ai, i=1,...,N. Рассмотрим задачу наилучшего в 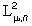приближения изображения 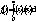изображениями (17), не требуя, чтобы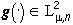

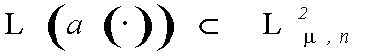(18)

Речь идет о задаче аппроксимации произвольного изображения 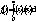изображениями, у которых яркость может быть произвольной функцией из 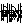, в то время, как цвет должен сохранять постоянное значение на каждом из заданных подмножеств A1,...,AN поля зрения X, (см. Лемму 3).

Так как

то минимум S (19) по 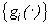достигается при

Рекомендуем скачать другие рефераты по теме: оформление доклада титульный лист, понятие культуры.



Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки