Предыдущая страница реферата | 5  6  7  8  9  10  11  12  13  14  15 | Следующая страница реферата

В заключение этого раздела вернемся к понятию формы изображения, заданного с точностью до произвольного, удовлетворяющего условиям физичности, преобразования яркости. Речь идет о форме изображения 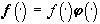, заданного распределением цвета 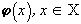, при произвольном (физичном) распределении яркости, например, 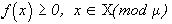. Для определения формы 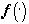рассмотрим задачу наилучшего в 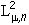приближения изображения 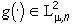такими изображениями

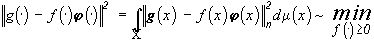,(41)

Теорема 5. Решение 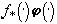задачи (41) дается равенством

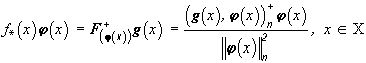,(42)

в котором 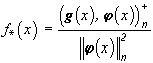, где 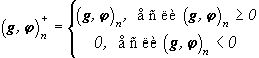. Невязка приближения

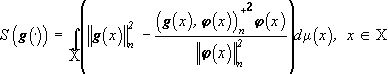,(43)

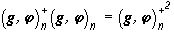( !)n

Определение. Формой изображения, заданного распределением цвета 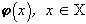, назовем выпуклый, замкнутый конус изображений

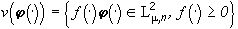
или - проектор 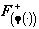на .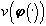

Всякое изображение g(× ), распределение цвета которого есть j (× ) и только такое изображение содержится в 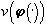и является неподвижной точкой оператора

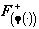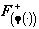: g(× ) = g(× ).(#)

Поскольку на самом деле детали сцены, передаваемые распределением цвета j (× ), не представлены на изображении f(× ) = f(× )j (× ) в той области поля зрения, в которой яркость f(x)=0, xÎ X, будем считать, что 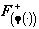- форма любого изображения f(x) = f(x)j (x), f(x)>0, xÎ X(modm ), все такие изображения изоморфны, а форма всякого изображения g(× ), удовлетворяющего уравнению (#), не сложнее, чем форма f(× ).

Замечание 5. Пусть j 1,..., j N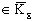 - исходный набор цветов, 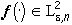, A1,...,AN - соответствующее оптимальное разбиение X, найденное в теореие 4 и

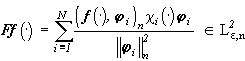,(34*)

- наилучшее приближение f(× ). Тогда в равенстве (24)

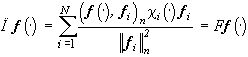,(24*)

если A1,...,AN - исходное разбиение X в теореме 3. Наоборот, если A1,...,AN - заданное в теореме 3 разбиение X и f1,...,fN - собственные векторы операторов Ф1,...,ФN (23) соответственно, отвечающие максимальным собственным значениям, то f1,...,fN и будет выполнено равенство (24), если в (34*) определить j i как цвет fi в (24), i=1,...,N.

Проверка этого замечания не представляет затруднений.

В. Случай, когда допускаются небольшие изменения цвета в пределах каждого Ai, i=1,...,N.

Разумеется, условие постоянства цвета на множествах Ai, i=1,...,N, на практике может выполняться лишь с определенной точностью. Последнюю можно повысить как путем перехода к более мелкому разбиению , так и допустив некоторые изменения цвета в пределах каждого Ai, i=1,...,N, например, выбрав вместо (17) класс изображений

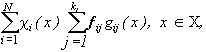(17*)

в котором 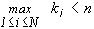в (3).

Поскольку в задаче наилучшего приближения f(× ) изображениями этого класса предстоит найти 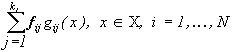, векторы 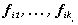при любом i=1,...,N, можно считать ортогональными, определив

,(*)

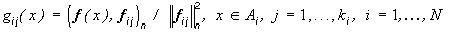Рекомендуем скачать другие рефераты по теме: оформление доклада титульный лист, понятие культуры.



Предыдущая страница реферата | 5  6  7  8  9  10  11  12  13  14  15 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки