Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

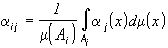,i=1,...,N, j=1,...,n,(12)

и искомое изображение (4) задается равенством

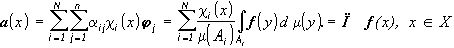.(13)

Оператор 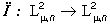является ортогональным проектором на линейное подпространство (4****) 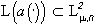изображений (4), яркости и цвета которых не изменяются в пределах каждого Ai , i=1,...,N.

Черно-белый вариант 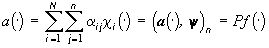(4*) цветного изображения 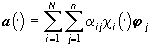(4) является наилучшей в 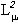аппроксимацией черно-белого варианта 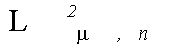цветного изображения f, если цветное изображение 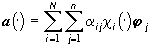(4) является наилучшей в 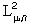аппроксимацией цветного изображения f. Оператор 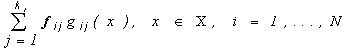, является ортогональным проектором на линейное подпространство черно-белых изображений, яркость которых постоянна в пределах каждого .

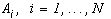В точках множества 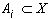цвет 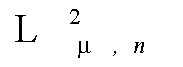(4**) наилучшей аппроксимации 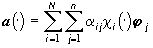(4) цветного изображения f (2) является цветом аддитивной смеси составляющих f излучений, которые попадают на .

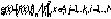Доказательство.Равенства (12) - условия минимума положительно определенной квадратичной формы (11), П - ортогональный проектор, поскольку в задаче (11) наилучшая аппроксимация - ортогональная проекция f на 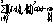. Второе утверждение следует из равенства

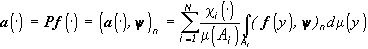, вытекающего из (13). Последнее утверждение следует из равенств

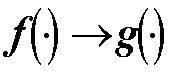
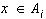,i=1,...,N вытекающих из (12) и равенства (1), в котором индекс k следует заменить на xÎ X. ¦

Замечание 1. Для любого измеримого разбиения 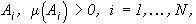ортогональные проекторы 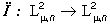и 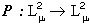определяют соответственно форму в широком смысле цветного изображения (4), цвет и яркость которого, постоянные в пределах каждого 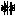, различны для различных 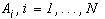, ибо 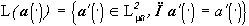, и форму в широком смысле черно-белого изображения, яркость которого постоянна на каждом 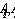и различна для разных 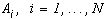,[2].

Если учесть, условие физичности (2*), то формой цветного изображения следует считать проектор 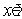на выпуклый замкнутый конус 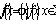(4***)

Аналогично формой черно-белого изображения следует считать проектор 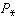на выпуклый замкнутый конус изображений (4*), таких, что 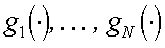[2]. Дело в том, что оператор 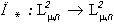определяет форму 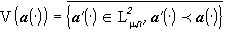изображения (4), а именно

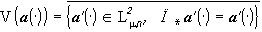- множество собственных функций оператора 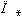. Поскольку 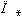f(× ) - наилучшее приближение изображения 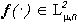изображениями из 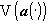, для любого изображения 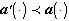из 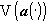и только для таких 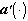- 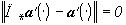. Поэтому проектор 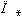можно отождествить с формой изображения (4).

Аналогично для черно-белого изображения a(× )

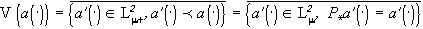, [2]. И проектор 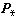можно отождествить с формой изображения (4*), как это сделано в работах [2,3].

Примечания.

Формы в широком смысле не определяются связью задач наилучшего приближения элементам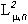и и 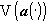, которая известна как транзитивность проецирования. Именно, если 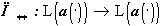оператор наилучшего в 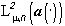приближения злементами выпуклого замкнутого 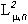(в и в 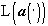) конуса 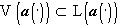, то 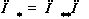. Иначе говоря, для определения наилучшего в 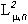приближения 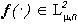элементами 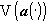можно вначале найти ортогональную проекцию 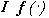изображения 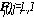на 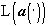, а затем 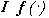спроецировать в 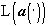на 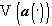. При этом конечномерный проектор 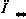для каждого конкретного конуса 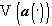может быть реализован методом динамического программирования, а для многих задач морфологического анализа изображений достаточным оказывается использование лишь проектора .

Форма в широком смысле 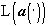(4***) изображения (4) полностью определяется измеримым разложением 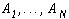, последнее, в свою очередь определяется изображением

,

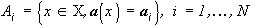если векторы 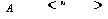попарно различны. Если при этом 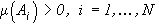, то форма в широком смысле 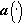может быть определена и как оператор ортогонального проецирования на 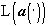, определенный равенством (13).

Посмотрим, каким образом воспользоваться этими фактами при построении формы в широком смысле как оператора ортогонального проецирования на линейное подпространство 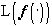(10*) для произвольного изображения 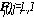. Пусть 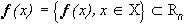- множество значени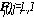й и 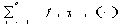- измеримое разбиение X , порожденное 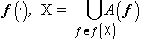, в котором 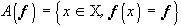- подмножество X , в пределах которого изображение 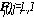имеет постоянные яркость и цвет, определяемые вектором 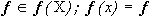, если .

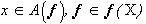Однако для найденного разбиения условие 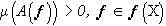, вообще говоря, невыполнимо и, следовательно, теорема 1 не позволяет построить ортогональный проектор на 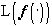. Покажем, что можно получить как предел последовательности конечномерных ортогональных проекторов. Заметим вначале, что любое изображение 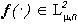можно представить в виде предела (в 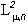) должным образом организованной последовательности мозаичных изображений

(*)

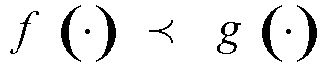где 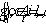- индикатор множества 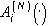, принадлежащего измеримому разбиению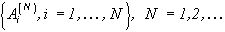

В (*) можно, например, использовать так называемую исчерпывающую последовательность разбиений [], удовлетворяющую следующим условиям

Рекомендуем скачать другие рефераты по теме: оформление доклада титульный лист, понятие культуры.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки