Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

3)

 группа

Следствие:

Произведение обратимых матриц есть обратимая матрица

Если  обратима, то обратима

§2 Элементарные матрицы

Пусть  поле скаляров

Определение.Элементарной матрицей называется матрица, полученная из единичной матрицы  в результате одного из следующих элементарных преобразований:

Умножение строки (столбца)  на скаляр

Прибавление к какой либо строке (столбцу)  другой строки (столбца), умноженный на скаляр

Обозначение: -элементарная матрица, полученная умножением на  -строки (столбца) матрицы

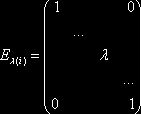
-строка

-элементарная матрица, полученная прибавлением к -строке (столбцу) матрицы  -строки (столбца), умноженной на

-строка

Пример: Элементарные матрицы порядка 2

, , , ,

Обозначение: -элементарная матрица, полученная из единичной матрицы с помощью элементарного преобразования

Глава IV

§1 Определители

Определитель матрицы обозначается . Другими словами определитель матрицы -это сумма произведений из множества  умноженная на знак, соответствующей подстановки.

Пример

Рекомендуем скачать другие рефераты по теме: доклад 6 класс, здоровый образ жизни реферат.



Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки