Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

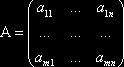
§1 Умножение матриц

,

,

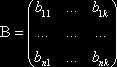
Опр. Произведением  матрицы  на  матрицу  называется  матрица . , где

, где

Говорят, что  есть скалярное произведение -строки матрицы  на -столбец матрицы .

, где

Пример:

§2 Свойства умножения матриц

Умножение матриц ассоциативно:

1)  , если определены произведения матриц  и

Доказательство:

Пусть , так как определено , то  и определено , то

Определим матрицы:

а)

б)

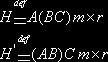 (1) матрицы, тогда  имеют одинаковую размерность

2) Покажем, что на одинаковых местах в матрицах  расположены одинаковые элементы

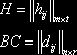из равенства (1) (2), (3). Подставляя (3) в (2) получим:

, тогда (4), (5). Подставляя (5) в (4) получим:

Вывод: Матрицы  имеют одинаковую размерность и на одинаковых местах расположены одинаковые элементы.

Умножение матриц дистрибутивно :

Рекомендуем скачать другие рефераты по теме: доклад 6 класс, здоровый образ жизни реферат.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки