Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Пусть -матрица , тогда -линейная комбинация строк матрицы  коэффициенты которой служат элементы матрицы

Пример:

Столбцы матрицы -линейная комбинация столбцов матрицы . Строки -линейная комбинация строк матрицы .

§4 Транспонирование произведения матриц

 поле скаляров, , , ,

Теорема

 если , то . Обозначим: ,

Доказательство:

 1) Пусть ,

 - размерности ,- размерности , тогда и имеют одинаковую размерность

2) , -элемента расположенный в -строке, -столбце матрицы  т.е

, -произведение -строки транспонированной  на  столбец ,

Глава III

§1 Обратимые матрицы

 поле скаляров, множество матриц порядка

Определение. Квадратная матрица  порядка  называется единичной матрицей ,

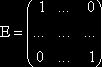
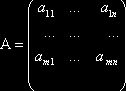
Пусть ,

Теорема 1

, то для  выполняется  

Доказательство:

 

Рекомендуем скачать другие рефераты по теме: доклад 6 класс, здоровый образ жизни реферат.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки