
Содержание и значение математической символики
Категория реферата: Рефераты по математике
Теги реферата: реферат на тему организация, доклад
Добавил(а) на сайт: Андроника.
Предыдущая страница реферата | 11 12 13 14 15 16 17 18 19 20 21 | Следующая страница реферата
Если мы теперь имеем булевы функции {F (xl, х2, ..., хn), G (х1, х2, ..., хn)} от n переменных, то действие связок над ними определяется естественным образом:
F (xl, x2, ..., хn) Ù G (х1, x2, ..., хn), F (xl, x2, ...,хn) Ú G (xl, x2, ..., хn), ùF (xl, x2, ..., хn) – это такие булевы функции, которые принимают значения, предписываемые соответствующими таблицами для каждого возможного значения аргументов. Кратко: булевы операции так переносятся на булевы функции, как действия арифметики переносятся на обычные функции числовых аргументов. Вообще имеет место далеко идущая аналогия между обычной алгеброй чисел и числовыми функциями, с одной стороны, и высказываниями и булевыми функциями – с другой. При этом можно отметить, что в одном определенном смысле алгебра булевых функций проще алгебры числовых функций: если рассматривать лишь функции некоторого конечного числа аргументов, то таких функций лишь конечное число. Поэтому выкладки с булевыми функциями вполне доступны пониманию школьников старших классов.
Естественно, закономерности булевой алгебры менее привычны и вызывают удивление и недоверие: это судьба всякого новшества.
Выпишем законы булевой алгебры. Большими латинскими буквами А, В, ..., X, Y, Z мы обозначим объекты, над которыми осуществляются булевы операции Ù, Ú, ù. Для определенности будем считать, что эти объекты – булевы функции некоторого фиксированного числа переменных. Среди них есть два особых элемента: 1, 0. Это соответственно функции, принимающие для всех аргументов значения 0 и 1 (постоянные функции – нуль и единица). Тогда
А Ù В = В Ù А, A Ú B = B Ú A
A Ù (В Ù C) = (А Ù В) Ù C A Ú (В Ú C) = (А Ú В) Ú C
A Ù A = A A Ú A = A
A Ù 1 = A A Ú 1 = A
A Ù 0 = 0 A Ú 0 = A
ù(A Ù B) = ùA Ú ùB ù(A Ú B) = ùA Ù ùB
A Ù (B Ú C) = (A Ù B) Ú (A Ù C) A Ú (B Ù C) = (A Ú B) Ù (A Ú C)
ù ùA = A
Если, как это обычно делают, булевы операции Ú, Ù, ù считать аналогом сложения, умножения и перехода к противоположному числу, то некоторые из вышеприведенных законов те же, что для числового сложения и умножения, другие же существенно отличаются от привычных.
4.1.3 Задания для учащихся.
Верно ли высказывание: ù(205 кратно 5); 7![]() 7; ù(8>10); 1£3£3.
7; ù(8>10); 1£3£3.
А – множество точек треугольника и В – множество точек четырехугольника.
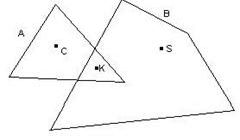
Верно ли высказывание: CÎA Ù CÎB; KÎB Ù KÎA; SÎB Ú SÎA; ù(SÎA)ÙSÎB?
Известно, что А=и, В=и, Х=л, Y=л. Найдите значение высказывания:
АÚùХ; ùYÙùA; AÞX; ù(ùВÚY); (AÙB)ÚX; (XÚB)ÞY; (XÙA)Þ(YÚB); ù (AÚX)Ù(YÚùX).
Составьте таблицу истинности высказываний: ùХÙХ; (ХÚY)ÚùY; (XÙY)ÚùX; ùXÞY; (XÙY)ÞY.
Используя переменные X, Y, Z, запишите сочетательное свойство операции «и».
Проверьте равенство (XÚY)ÙZ º (XÙZ)Ú(YÙZ) и (XÙY)ÚZº(XÚZ)Ù(YÚZ), составляя таблицы истинности для левой и правой части.
4.2 Предикаты и кванторы.
4.2.1 Предикаты.
Алгебра предикатов – тот раздел математической логики, который непосредственно надстраивается над алгеброй высказываний.
Как мы видели, одной из основных задач алгебры высказываний является изучение истинности или ложности высказываний в зависимости от истинности или ложности входящих в них высказываний. Несмотря на большую важность этой области логики, она оказывается слишком бедной для описания и для изучения даже простейших заключений науки и практики. В рамки алгебры высказываний не укладываются ни простейшие заключения арифметики и геометрии, не говоря уже о довольно сложных логических выводах, с которыми мы сталкиваемся в других науках и в повседневной жизни.
Действительно, рассмотрим следующие простейшие заключения.
Рекомендуем скачать другие рефераты по теме: образ сочинение, реферат бесплатно без регистрации.
Предыдущая страница реферата | 11 12 13 14 15 16 17 18 19 20 21 | Следующая страница реферата