Сопряжённые числа
Категория реферата: Рефераты по математике
Теги реферата: шпоры по истории россии, реферат государственный
Добавил(а) на сайт: Устимович.
Предыдущая страница реферата | 5 6 7 8 9 10 11 12 13 14 15 | Следующая страница реферата
Рекуррентные соотношения типа (6) возникают не только в теории чисел, но и в разных задачах анализа, теории вероятностей. Вот характерный пример комбинаторной задачи такого типа (она предлагалась на последней международной олимпиаде в Лондоне):
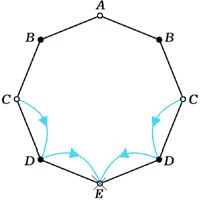
7 (М595). В вершине A правильного восьмиугольника сидит лягушка. Из любой вершины восьмиугольника, кроме вершины E, противоположной A, она может прыгнуть в любую из двух соседних вершин. Попав в E, лягушка останавливается и остаётся там. Найти количество em различных способов, которыми лягушка может попасть из вершины A в E ровно за m прыжков.
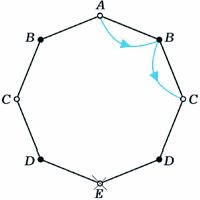
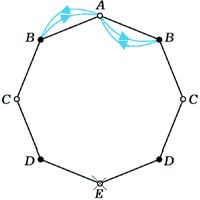
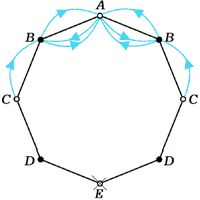
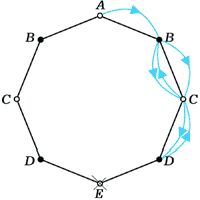
Если раскрасить вершины восьмиугольника через одну в чёрный и белый цвет (рис. 2), сразу станет ясно, что e2k–1 = 0 при любом k: цвет вершин при каждом прыжке меняется. Обозначим через an и cn количество способов, которым лягушка может за 2n прыжков, попасть из вершины A, соответственно, в вершину A и в одну из вершин C (из соображений симметрии ясно, что в каждую из вершин, обозначенных на рисунке буквой C, можно попасть одним и тем же числом способов). Как легко проверить (см. рис.2а,б,в,г),
a1 = 2, c1 = 1;
|
(7) |
А интересующее нас число e2n равно, очевидно, 2cn–1 (рис. 2д).
|
а) c1 = 1 |
б) a1 = 2 |
в) an+1 = 2an + 2cn |
|
г) cn+1 = an + 2cn |
д) e2n = 2cn–1 |
|
Рис. 2. а) |
Из A в C за два прыжка можно попасть только одним способом: c1 = 1. |
||||
|
б) |
Из A в A за два прыжка можно попасть двумя способами: a1 = 2. Рекомендуем скачать другие рефераты по теме: ответы по биологии, сочинение ревизор. Предыдущая страница реферата | 5 6 7 8 9 10 11 12 13 14 15 | Следующая страница реферата Поделитесь этой записью или добавьте в закладкиКатегории: |