Сопряжённые числа
Категория реферата: Рефераты по математике
Теги реферата: шпоры по истории россии, реферат государственный
Добавил(а) на сайт: Устимович.
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 11 | Следующая страница реферата
Мы уже говорили о пользе симметрии в геометрических задачах. Своего рода симметрией в алгебре является замена плюса на минус.
Так, если какое-либо выражение от √d равно p + q√d и мы всюду в этом выражении заменим √d на –√d, то естественно ожидать, что новое выражение окажется равным сопряженному числу p – q√d. Мы будем пользоваться таким очевидным частным случаем этого свойства (a и b — рациональны, √d — нет):
|
(a + b√d)n = p + q√d => (a – b√d)n = p – q√d. |
(4) |
5. Доказать, что уравнение
(x + y√5)4 + (z + t√5)4 = 2 + √5
не имеет решений в рациональных числах x, y, z, t.
Можно, конечно, найти отдельно сумму членов левой части, не содержащих √5 (она должна быть равна 2), и отдельно — коэффициент при √5 (он должен равняться 1). Но что делать с полученной громоздкой системой неясно. Вместо этого воспользуемся (4) и заменим плюс перед √5 на минус!
(x – y√5)4 + (z – t√5)4 = 2 – √5.
Слева стоит неотрицательное число, справа — отрицательное.
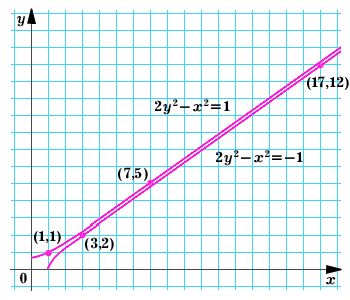
6. Доказать, что существует бесконечно много пар (x; y) натуральных чисел, для которых x2 отличается от 2y2 на 1:
|
| x2 – 2y2 | = 1. |
(5) |
Несколько таких пар с небольшими (x; y) легко найти подбором: это (1; 1), (3; 2), (7; 5), (17; 12), ... (рис. 1). Как продолжить этот набор? Можно ли записать общую формулу для этих решений?
|
Рис. 1. Проходят ли эти гиперболы через бесконечное число узлов клетчатой бумаги? |
Найти ответы на эти вопросы нам поможет число 1 + √2. Закономерность, позволяющая получать всё новые и новые решения (x; y), указана в таблице:
|
n |
(1 + √2)n |
xn |
yn |
xn2 – 2yn2 |
(1 – √2)n |
|
1 Рекомендуем скачать другие рефераты по теме: ответы по биологии, сочинение ревизор. Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 11 | Следующая страница реферата Поделитесь этой записью или добавьте в закладкиКатегории: |