Предыдущая страница реферата | 3  4  5  6  7  8  9  10  11  12  13 | Следующая страница реферата

Любое подмножество малого множества является малым, любое надмножество большого – большим.

Объединение двух малых множеств является малым, пересечение дух больших множеств – большим.

Всякое конечное множество является малым, всякое множество, имеющее конечное дополнение – большим.

С помощью такого ультрафильтра построим искомое неархимедово расширение поля действительных чисел.

Будем говорить, что последовательности  эквивалентны, если равенство  “выполнено почти при всех i“, т.е. Если множество тех i, при которых , большое. Согласно свойству 5 любые последовательности, отличающиеся в конечном числе членов, эквивалентны. С каждой последовательностью сопоставим ее класс эквивалентности – класс всех эквивалентных ей последовательностей. Получающиеся классы эквивалентности будут называться гипердействительными числами. Обыкновенные действительные числа вкладываются в множество гипердействительных чисел. Таким образом, *R оказывается, как мы того и хотели, расширением множества R.

Определим сложение и умножение на гипердействительных числах. Пусть класс  содержит последовательность , класс  – последовательность . Назовем суммой классов  и  класс, содержащий последовательность ,а произведением последовательность . Корректность этих определений обеспечивается свойством 4 из определения ультрафильтра.

Итак, мы ввели на множестве гипердействительных чисел сложение, умножение и порядок. Нетрудно проверить, что мы получили упорядоченное поле, т.е. что во множестве гипердействительных чисел выполняются все обычные свойства сложения, умножения и порядка. Аксиома Архимеда, однако, в этом поле не выполняется.

Не знаю, как назвать

А теперь посмотрим, как ведут себя расширения операторов.

Теорема 1:

Доказательство:

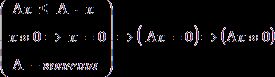
Пусть . Это внутреннее множество. Внутренне числовое множество имеет супремум. Пусть . Если М – конечен, то А – ограничен. Если М – бесконечен, то  такой, что , но , то есть  – бесконечна. Рассмотрим , но, с другой стороны, . Получили противоречие, если предположить, что норма бесконечна. Значит оператор А ограничен.

Доказано.

Теорема 2:

Доказательство:

Пусть есть операторы А и А1 такие, что

.

Воспользуемся теоремой:

Если оператор  и обратим, а так же есть оператор В такой, что , то А1 – обратим, причём .

Поскольку данные операторы бесконечно близки, то норма их разности есть число бесконечно малое. А норма оператора А – конечна, а бесконечно малое число, естественно, меньше числа, обратного конечному, что гарантирует выполнение неравенства . Поэтому оператор В тоже обратим. Оценим норму , воспользуемся вторым неравенством:  – конечна, , от сюда , то . Так как мы поняли, что оператор А1 обратим, то это неравенство можно записать по-другому:

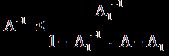, от куда получим . Имеем одновременное выполнение двух неравенств:  и , то есть , откуда . Что и требовалось доказать.

Доказано.

Определение резольвенты в этом поле такое же, как и в стандартном. Но есть некоторое расхождение в определении спектра и собственного вектора.

Спектром линейного оператора в  называется множество:

Рекомендуем скачать другие рефераты по теме: правовые рефераты, задачи с ответами.



Предыдущая страница реферата | 3  4  5  6  7  8  9  10  11  12  13 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки