Предыдущая страница реферата | 3  4  5  6  7  8  9  10  11  12  13 | Следующая страница реферата

если , , то .

В таком случае говорят, что введенный порядок превращает Р в упорядоченное поле. Упорядоченное поле Р является неархимедовым тогда и только тогда, когда в нём есть положительные бесконечно малые элементы. Упорядоченное поле Р называется расширением поля действительных чисел R, если Р содержит все действительные числа и, кроме того, операции и порядок из Р, рассматриваемые на элементах их R, совпадают с обычными арифметическими операциями и обычным порядком на действительных числах.

Пример неархимедовой числовой системы

Построим пример неархимедова упорядоченного поля, являющегося расширением поля действительных чисел.

Предположим, что искомое расширение *R уже построено, и исследуем его строение. Элементы множества *R мы будем называть гипердействительными числами. Среди них содержатся и все действительные числа. Чтобы отличить их, будем называть действительные числа (элементы R) стандартными, а остальные гипердействительные числа (элементы *R/R)—нестандартными.

По нашему предположению, поле *R содержит бесконечно малые числа, не равные нулю. Гипердействительное число  называется бесконечно малым, если все суммы

   и т. д.

меньше 1. Здесь через обозначен модуль гипердействительного числа , определяемый так:  .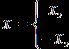

Отметим, что стандартное число 0 также оказывается, согласно этому определению, бесконечно малым. Но все остальные бесконечно малые числа не могут быть стандартными. Это следует из того, что для стандартных чисел справедлива аксиома Архимеда.

Наряду с бесконечно малыми в поле *R существуют и бесконечно большие. Мы называем гипердействительное число А бесконечно большим, если

 и т.д.

Если,  бесконечно мало, но отлично от нуля, то число  бесконечно велико. Верно и обратное, если число А бесконечно велико, то число  бесконечно мало. Отсюда следует, что все бесконечно большие числа нестандартны.

Гипердействительные числа, не являющиеся бесконечно большими, называются конечными. Каждое конечное гипердействительное число  можно представить в виде  где  – стандартное число, а  –- бесконечно малое. Пусть  – конечное гипердействительное число. Разобьём действительные числа на два класса: меньшие  и большие . Т.к.  конечно, то оба класса не пусты. По “аксиоме полноты“ существует действительное число , разделяющее эти классы. Легко видеть, что  будет бесконечно малым. Число  называется стандартной частью конечного гипердействительного числа . Обозначается это так:. Таким образом, множество конечных гипердействительных чисел разбивается на классы. Эти классы называются монадами. Монадой стандартного числа  называется множество всех бесконечно близких к нему гипердействительных чисел.

Обсудив структуру нестандартного “микромира”, скажем несколько слов о строении нестандартного “макромира”. Их можно разбить на классы (“галактики”), каждый из которых устроен, подобно множеству всех конечных гипердействительных чисел. Среди галактик нет ни самой большой, ни самой малой; между любыми двумя галактиками есть бесконечно много других галактик.

Что ещё нужно знать о бесконечно малых?

Рассмотрим, что получается в результате построения поля гипердействительных чисел.

Прежде всего, мы получаем неархимедово расширение поля действительных чисел. Кроме того, “каждому объекту стандартного мира” поставлен в соответствие его аналог в “нестандартном мире”. Именно нестандартным аналогом любого действительного числа является оно само; любому подмножеству А множества R соответствует подмножество *А множества *R, каждой функции f из R в R соответствует функция *f из *R в *R, каждой двуместной функции g из R в R соответствует функция *g из *R в *R и т. д. Разумеется, эти аналоги *A, *f, *g не произвольны, а должны обладать некоторыми специальными свойствами: так, *А, на действительных числах f и *f совпадают, так что *f является продолжением для f, а *g – продолжением для g. При этом оказывается выполненным так называемый принцип переноса, утверждающий, грубо говоря, что в стандартном универсуме истинны те же утверждения формального языка, что и в нестандартном универсуме. Типичное использование состоит в том, что мы доказываем желаемый результат в нестандартном универсуме, а потом, заметив, что результат выразим в языке, заключаем, что он выполнен также в стандартном универсуме.

Приведем два примера “нестандартных определений” стандартных понятий. Пусть  – последовательность действительных чисел, или, другими словами, функция из N в R. Её нестандартный аналог представляет собой функцию из *N в *R; значение этой функции на гипернатуральном числе m естественно обозначать .

Определение предела. Стандартное число  называется пределом последовательности , если все бесконечно далекие члены этой последовательности бесконечно близки к , т.е. для всякого нестандартного гипернатурального числа  разность  бесконечно мала.

Определение предельной точки. Стандартное число называется предельной точкой последовательности , если некоторые бесконечно далёкие члены последовательности бесконечно близки к , т.е. существует такое нестандартное гипернатуральное число , что разность бесконечно мала.

А теперь докажем эквивалентность «нестандартного» определения предела последовательности «стандартному», пользуясь принципом переноса:

Доказательство:

Пусть , что обозначает

Рекомендуем скачать другие рефераты по теме: правовые рефераты, задачи с ответами.



Предыдущая страница реферата | 3  4  5  6  7  8  9  10  11  12  13 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки