Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Так как <1, то .Пространство Е полно, так что из сходимости ряда  вытекает, что сумма ряда  представляет собой ограниченный линейный оператор. Для любого n имеем

;

переходя к пределу при  и учитывая, что , получаем

,

что и означает, что .

Доказано.

Теорема 7. Если А – ограниченный линейный оператор в банаховом пространстве и >, то  – регулярная точка.

Доказательство:

Так как, очевидно, что ,

то

При < этот ряд сходится (см. теорему 5), т.е. оператор  имеет ограниченный обратный. Иначе говоря, спектр оператора А содержится в круге радиуса  с центром в нуле.

Доказано.

Из выше доказанной теоремы вытекает разложение резольвенты в ряд Лорана на бесконечности

При < этот ряд сходится. Но  – это наименьшее из чисел С, удовлетворяющих неравенству:

Аf=Cf, если С – собственное значение, то и , то для наибольшего по модулю из собственных значений неравенство будет иметь место, с другой стороны, это число будет наименьшим. Следовательно, ряд  будет сходиться при <(А), где (А) – наибольший модуль собственных значений оператора А. Величина (А) называется спектральным радиусом оператора А.

Теорема 8: (А)=.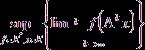

Для доказательства воспользуемся теоремой Коши-Адамара, сформулируем её. Теорема Коши-Адамара: Положим , . Рассмотрим степенной ряд . Тогда он сходится всюду в круге  и расходится всюду вне этого круга.

Доказательство:

Рассмотрим разложение резольвенты в ряд Лорана как степенной ряд:

.

По теореме Коши-Адамара его радиус сходимости равен числу

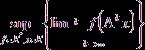, но с другой стороны радиус сходимости ряда Лорана резольвенты есть спектральный радиус.

Рекомендуем скачать другие рефераты по теме: правовые рефераты, задачи с ответами.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки