Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Теорема: Пусть ограниченный линейный оператор А0, отображающий банахово пространство Е на банахово пространство Е1, обладает ограниченным обратным  и пусть  – такой ограниченный линейный оператор, отображающий Е в Е1, что . Тогда оператор А= отображает Е на Е1 и обладает ограниченным обратным.

Теорема: Пусть Е – банахово пространство, I – тождественный оператор в Е, а А – такой ограниченный линейный оператор, отображающий Е в себя, что норма . Тогда оператор  существует, ограничен и представляется в виде

.

Резольвента линейного оператора

Определение и примеры резольвенты оператора

Рассмотрим оператор А, действующий в (комплексном) линейном топологическом пространстве Е, и уравнение

Ах=

Решения этого уравнения зависят от вида оператора . Имеется три возможности:

уравнение Ах= имеет ненулевое решение, т.е.  есть собственное значение для А; оператор  при этом не существует;

существует ограниченный оператор , т.е.  есть регулярная точка;

оператор  существует, т.е. уравнение Ах= имеет лишь нулевое решение, но этот оператор не ограничен.

Введём следующую терминологию. Оператор  называется резольвентой оператора А. Число  мы назовём регулярным для оператора А, действующего в линейном топологическом пространстве Е, если оператор  определён на всём Е и непрерывен, множество таких  будем называть резольвентным множеством и обозначать . Совокупность всех остальных значений  называется спектром оператора А, будем обозначать . Спектру принадлежат все собственные значения оператора А, так как если х=0 при некотором , то  не существует. Их совокупность называется точечным спектром. Остальная часть спектра, т.е. совокупность тех , для которых  существует, но не непрерывен, называется непрерывным спектром. Итак, каждое значение  является для оператора А или регулярным, или собственным значением, или точкой непрерывного спектра. Возможность наличия у оператора непрерывного спектра – существенное отличие теории операторов в бесконечномерном пространстве от конечномерного случая.

В конечномерном же случае имеется лишь две первые возможности. Причём,  называется собственным значением оператора, если данное уравнение имеет ненулевое решение. Совокупность всех собственных значений образуют спектр оператора, а все остальные значения называются  – регулярными. Иначе, говоря , есть регулярная точка, если оператор  обратим.

Рассмотрим насколько примеров резольвент операторов.

Пример 1: Возьмём оператор, переводящий конечномерное пространство в конечномерное, как было сказано выше, его можно задать матрицей коэффициентов:

, тогда

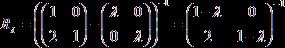
С помощью нехитрых преобразований находим обратную матрицу, тем самым резольвенту этого оператора:

,

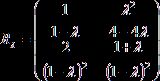здесь хорошо видно, что оператор, заданный этой матрицей не существует при =1, то есть это собственное значение оператора А.

Пример 2: Рассмотрим линейный оператор, отображающий пространство непрерывных функций на отрезке [a,b] на себя. Пусть это будет оператор умножения на функцию g(x). Тогда резольвента этого оператора запишется в следующем виде: , такой оператор непрерывен, если функция g(x) не принимает значение  на отрезке [a,b], в противном случае  будет являться собственным значением. То есть спектр этого оператора состоит из значений функции g(x) на отрезке [a,b]. Причём этот оператор имеет лишь непрерывный спектр, так как резольвента при  существует, но не непрерывна. Точечного спектра оператор не имеет.

Пример 3: Рассмотрим оператор дифференцирования на множестве дифференцируемых функций. А: (для краткости будем писать вместо f(x) просто f). Рассмотрим резольвенту этого оператора: , то есть мы должны найти обратный оператор к оператору: , для чего надо решить дифференциальное уравнение относительно . Решим уравнение  методом Бернулли:

;

;

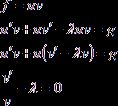; ; ; ; , откуда ,

Рекомендуем скачать другие рефераты по теме: правовые рефераты, задачи с ответами.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки