Предыдущая страница реферата | 24  25  26  27  28  29  30  31  32  33  34 | Следующая страница реферата

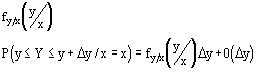
тут мы использовали второе определение одномерной плотности.

В качестве условной плотности вероятности используется следующее выражение

Обоснование выражения для условной плотности вероятности

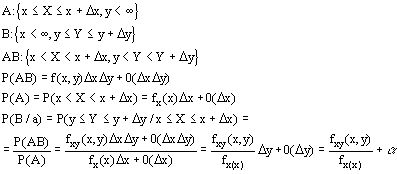
Выведем выражение для 

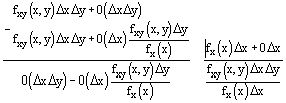
Обозначим

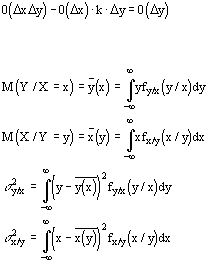
Условное мат. ожидание и дисперсия линии регрессии - зависимость Y от X, выраженная в изменении средних значений Y при переходе x от одного значения к другому. Найдем математическое ожидание MZ, где

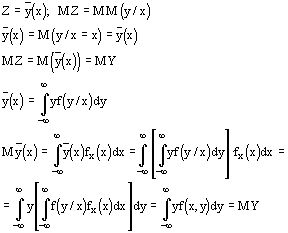
Двумерные независимые случайные величины (двумерные дискретные случайные величины)

Двумерная дискретная случайная величина называется случайной величиной с независимыми компонентами, если

Показать самим, что справедливо

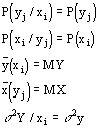
Доказать самим, что если испытание, исходом которого является пара чисел является композицией двух независимых испытаний, то случайные величины X Y независимы.

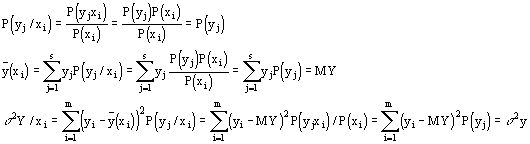
Независимые непрерывные двумерные случайные величины.

Непрерывными случайными величинами с независимыми компонентами называются если:

Непрерывная двумерная случайная величина имеет независимые случайные компоненты, если

или

Покажем, что второе эквивалентно первому.

Покажем, что если двумерная непрерывная случайная величина XY порождена композицией независимых испытаний, то X и Y независимы.

В силу определения независимых испытаний в композиционном пространстве

В силу определения независимых испытаний в композиционном пространстве A и B независимы.

Следовательно:

Многомерные дискретные случайные величины

Это система, состоящая из m дискретных одномерных случайных величин. Всю арифметику проделать самостоятельно.

Многомерные непрерывные случайные величины.

Система из m одномерных непрерывных случайных величин, у которой пространством элементарных событий является m-мерное арифметическое пространство либо его область, имеющая ненулевой объем.

m-мерная плотность вероятности удовлетворяет выражению

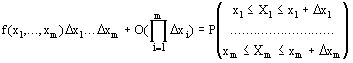
m-мерной функцией распределения называется числовая скалярная функция m действительных аргументов, которая численно равна:

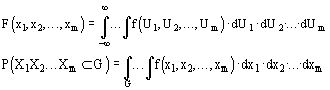
Случайные величины x1, x2, ... xm независимы, если

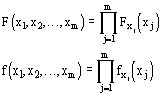
Доказать, что если m-мерная случайная величина порождена композицией m-мерных испытаний, то события независимы.

Запишем аналог формул

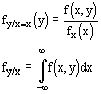
для многомерного случая.

Для получения плотности вероятности необходимо n-мерную плотность проинтегрировать в бесконечных пределах по переменным, которые соответствуют случайным величинам, не входящим в

Найдем плотность n-мерной случайной величины.

Рекомендуем скачать другие рефераты по теме: изложение по русскому 6 класс, реферат анализ.

Предыдущая страница реферата | 24  25  26  27  28  29  30  31  32  33  34 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки