Предыдущая страница реферата | 24  25  26  27  28  29  30  31  32  33  34 | Следующая страница реферата



Пример.

X - случайная величина, имеющая нормальное распределение с нулевым мат.ожиданием

Y=X2 (Y и X связаны функционально).

Найдем

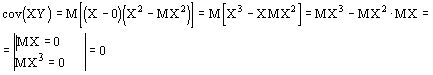
Случайная величина называется нормированной случайной величиной, ее мат.ожидание равно 0, а дисперсия -1.

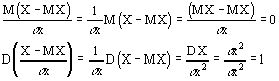
Коэффициентом корреляции случайных величин X и Y - это число

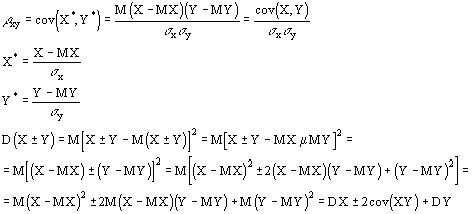
Следствие:

Если X и Y независимы, то коэффициент ковариации равен 0, то

Доказать, если независимы, то

 

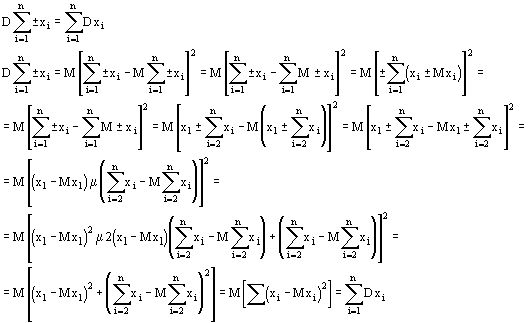
Свойства коэффициента корреляции

1.

По определению

т.к. всегда неотрицательна, то

2. Если , то с вероятность 1 X и Y связаны линейно.

Рассмотрим X*-Y*, отсюда M(X*-Y*)=0.

Если X и Y дискретные случайные величины, и дисперсия равна 0, то их сумма (разность) является постоянной

Пусть X и Y непрерывные случайные величины, то в соответствии с неравенством Чебышева

т.к.

Это неравенство и обозначает, что с вероятностью 1

откуда y=ax+b, где

Если коэффициент корреляции , то результаты опыта лежат на прямой

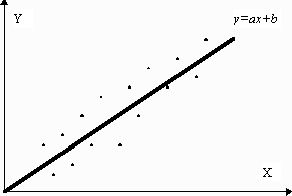
В общем случае Y можно представить в виде

Коэффициент корреляции является мерой близости линейной связи между случайными величинами X и Y: чем ближе коэффициент корреляции по модулю к 1, тем более тесно результаты конкретного испытания над X и Y соотносятся с прямой ax+b.

Нахождение плотности вероятности суммы двух независимых случайных величин

Дискретный случай.

Пусть X и Y - две дискретные независимые величины данного испытания и Z=X+Y. Возможное значение Z=z=x+y всегда представляет сумму двух возможных значений слагаемых X=x и Y=y. По правилу сложения

где суммирование распространено на те пары, которые в сумме дают Z. В силу независимости X и Y

Приняв во внимание, что y=z-x

Рекомендуем скачать другие рефераты по теме: изложение по русскому 6 класс, реферат анализ.

Предыдущая страница реферата | 24  25  26  27  28  29  30  31  32  33  34 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки