Рефераты | Рефераты по эргономике | О некоторой общей схеме формирования критериев оптимальности в играх с природой |
qn |
называется
матрицей рисков. В последней строке указаны вероятности состояний природы qj, j
= 1, …, n. Так как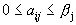 
(правое
неравенство следует из (1)), то из (2) получаем, что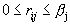 
.
Вероятность
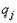состояния
природы Пj является очевидно вероятностью выигрыша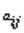 
и риска 
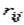при каждой
стратегии Ai, i = 1, …, m.Поэтому каждую стратегию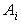 
можно
интерпретировать как дискретную случайную величину, которая может принимать
значения, равные выигрышам ai1, …, ain или рискам ri1, …, rin с
соответствующими вероятностями q1, …, qn.
Задача игрока А состоит в выборе из возможных стратегий Ai, ..., Am оптимальной. Таким образом, речь идет о решении задачи в чистых стратегиях ([1], с. 502, 508). Оптимальность стратегии понимают в различных смыслах и выбирают ее по различным критериям. Отметим, например, классические критерии Байеса ([2], с. 119*; [3], с. 46), Лапласа ([1], с. 500; [2], с. 119; [4], с. 103), Вальда ( [1], с. 504; [3], с. 91; [5], с. 56), Сэвиджа ([1], с. 504; [3], с. 92; [5], с. 57), Гурвица ([1], с. 505; [2], с. 120; [3], с. 47; [5], с. 57).
Цель настоящей статьи – предложить некоторую общую схему формирования критериев выбора оптимальных стратегий, на основе которой можно выделить некоторые классы критериев, включающие в себя отмеченные классические критерии и дающие возможность получать новые критерии оптимальности.
Результат игры в общем случае зависит от трех числовых параметров: выигрышей а игрока А, рисков r, которые появляются при выборе игроком А той или иной стратегии, и вероятностей q сoстояний природы. Желание "свернуть" эти три параметра в один показатель приводит к некоторой числовой функции, зависящий от этих трех параметров. Обозначим ее G(a, r, q) и назовем функцией игры. Характер зависимости функции игры G от а, r и q мотивируется логикой применяемого критерия. Значения
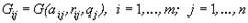
функции игры назовем показателями игры. Эти показатели образуют матрицу игры
|
Пj Ai |
П1 |
П2 |
... |
Пn |
||||
|
|
A1 |
G11 |
G12 |
... |
G1n |
|||
|
(Gij) = |
A2 |
G21 |
G22 |
... Рекомендуем скачать другие рефераты по теме: цель реферата, ответы по контрольной. Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 11 | Следующая страница реферата Поделитесь этой записью или добавьте в закладкиКатегории: |
