Аппроксимация непрерывных функций многочленами Содержание

Введение

I. Постановка основной задачи теории аппроксимации

1.1. Основная теорема аппроксимации в линейном нормированном пространстве

1.2. Теорема аппроксимации в пространстве Гильберта

1.3. Первая теорема Вейерштрасса

1.4. Вторая теорема Вейерштрасса

II. Круг идей П.Л. Чебышева

2.1. Теорема Валле-Пуссена и теорема существования

2.2. Теорема Чебышева

2.3. Переход к периодическим функциям

2.4. Обобщение теоремы Чебышева

III. Методы аппроксимации

3.1. Приближение функции многочленами

3.2. Формула Тейлора

3.3. Ряды Фурье

Заключение

Литература

Введение

Элементы важной и интересной области математики- теория приближения функций. Под приближением функции понимают замену по определенному правилу одной функции другой, близкой к исходной в том или ином смысле. Практическая необходимость в такой замене возникает в самых различных ситуациях, когда данную функцию необходимо заменить более простой и удобной для вычислений, восстановить функциональную зависимость по экспериментальным данным, и т.п.

Основоположником теории аппроксимации функций является великий русский математик Пафнутий Львович Чебышев (1821-1894).

В качестве приближающих функций выбирают чаще всего алгебраические и тригонометрические многочлены. Так же важное значение имеет метод наилучшего приближения, предложенный Чебышевым. Он возник из решения практических задач, связанных с конструированием прямолинейно направляющих шарнирных механизмов. Такие механизмы в XIX веке использовались в паровых машинах- основных универсальных двигателях того времени- для поддержания прямолинейного движения поршневого штока. К ним относятся параллелограмм Уатта и некоторые его разновидности.

На дальнейшее развитие этой теории оказало влияние открытие, сделанное в конце XIX века немецким математиком Карлом Вейерштрассом. Им была доказана принципиальная возможность приближения произвольной непрерывной функции с любой заданной степенью точности алгебраическим многочленом, что явилось второй причиной применения этих многочленов как универсального средства приближения функций, с заданной сколь угодно малой ошибкой.

Кроме алгебраических многочленов, другим средством приближения функций являются тригонометрические многочлены, значение которых в современной математике, конечно, не исчерпывается указанной ролью.

I. Постановка основной задачи аппроксимации

Основную задачу теории аппроксимации можно сформулировать следующим образом: на некотором точечном множестве 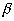в пространстве произвольного числа измерений заданы 2 функции f(P) и F(P,A1,A2...An) от точки P, из которых вторая зависит ещё от некоторого числа параметров А1,А2...Аn; эти параметры требуется определить так, чтобы уклонение в 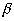функции F(P,A1,A2...An) от функции f(P) было наименьшим. При этом, конечно, должно быть указано, что понимают под уклонением F от f или, как ещё принято говорить, под расстоянием между F и f.

Если, например, рассматриваются ограниченные функции, то в качестве расстояния между двумя функциями можно взять верхнюю грань в 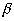модуля их разности. При таком определении расстояния для совокупности всех ограниченных в 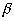функций оказываются справедливыми многие соотношения, которые мы имеем для точек обычного 3х-мерного пространства.

Последнее обстоятельство, с которым постоянно приходится сталкиваться в математике при рассмотрении других классов функций и многих иных совокупностей (множеств), привело к созданию весьма важного понятия метрического пространства, так что при дальнейшем изложении совокупность - это метрическое, либо Гильбертово пространство.

Рекомендуем скачать другие рефераты по теме: поняття реферат, дипломная работа школа.



1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки