История статистики
Категория реферата: Рефераты по математике
Теги реферата: рассказы, промышленность реферат
Добавил(а) на сайт: Felicata.
Предыдущая страница реферата | 22 23 24 25 26 27 28 29 30 31 32 | Следующая страница реферата
Рефераты | Рефераты по математике | История статистики |
-2 |
2 |
|||
|
49 - 50 |
50 |
0 |
5 |
0 |
0 |
|
50 - 51 |
20 |
+1 |
2 |
2 |
2 |
|
51 - 52 |
10 |
+2 |
1 |
2 |
4 |
|
Итого: |
100 |
– |
10 |
2 |
8 |
1. Средний вес пачки чая по выборке:
= 
´ K + x0 = 
´ 1 + 49,5 = 49,7 г.
2. Выборочная дисперсия веса пачки чая:
σ2 =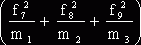 
= 
= 0,76.
3. Средняя ошибка выборочной средней:
= 
= 
= 0,087 г.
4. Предел для ошибки с вероятностью 0,954:
D = 2m = 0,174 г » 0,2 г.
5. Границы генеральной средней:
= ± D = 49,7 ± 0,2 г.
Таким образом, с вероятностью 0,954 можно утверждать, что вес пачки чая в среднем для всей партии не более 49,9 г и не менее 49,5 г.
Определение объема выборки при заданной ее точности является проблемой, обратной рассмотренной нами - определению ошибки выборки при данном ее объеме. Формула объема выборки получается из соответствующей формулы предельной ошибки. Так, получаем для индивидуального бесповторного отбора:
n =
;
группового бесповторного отбора:
r =
.
При решении задач на определение необходимого объема выборки следует иметь в виду, что вместо генеральной дисперсии определенного вида берется ее оценка - примерное значение, полученное из того или иного источника. Рассмотрим следующий общий пример.
Пример. Нужно определить абсолютный и относительный объемы индивидуального отбора для исследования генеральной доли, чтобы ошибка частости с вероятностью 0,954 не превышала 0,02, если выборка производится из генеральной совокупности объема: а) 1000; б) 100000 единиц.
Используя формулу n =
, в которой полагаем t = 2 (гарантийная вероятность равна
0,954), а pq = 0,25, имеем:
а) n = 
= 714, или 71,4%;
б) n = 
= 2439, или 2,44%.
Тема 11. Законы распределения
Конечной целью обработки информации методами математической статистика, если речь идет о больших выборках, является получение закона распределения исследуемой случайной величины. Это связано с тем, что закон распределения является фактически, тем аппаратом, который позволяет определить вероятность появления (или, наоборот, непоявления) случайной величины в тот или иной период времени или вероятность того, что случайная величина попадет в тот или иной интервал ее возможных значении. Этот этап статистической обработки является одним из наиболее важных, так как ошибка при выборе того или иного закона распределения приводит к ошибкам при дальнейшем решении практических задач.
Если проанализировать все этапы статистической обработки, то можно сделать вывод, что влекущими за собой наиболее существенные ошибки, а, следовательно, наиболее ответственными, являются этапы, на которых решаются следующие задачи:
1. Возможно ли объединение нескольких малых или средних выборок в одну.
2. Отбрасывать или учитывать резко отличающиеся результаты.
Рекомендуем скачать другие рефераты по теме: сеть рефератов, бесплатные рассказы.
Предыдущая страница реферата | 22 23 24 25 26 27 28 29 30 31 32 | Следующая страница реферата