Предыдущая страница реферата | 5  6  7  8  9  10  11  12  13  14  15 | Следующая страница реферата

Форма ИК компоненты f(× ) может быть определена лишь тогда, когда известно множество возможных преобразований j 2(× ) f2(× ).

Некоторые применения.

Задачи идентификации сцен.

Рассмотрим вначале задачи идентификации сцен по их изображения, неискаженным геометрическими преобразованиями, поворотами, изменениями масштаба и т.д. Ограничимся задачами, в которых предъявляемые для анализа изображения получены при изменяющихся и неконтролируемых условиях освещения и неизвестных и, вообще говоря, различных оптических характеристиках сцены.

1). Задачи идентификации при произвольно меняющейся интенсивности освещения.

Можно ли считать f(× ) и g(× ) изображениями одной и той же сцены, возможно, отличающимя лишь распределениями яркости, например, наличием теней?

В простейшем случае для идентификации достаточно воспользоваться теоремой 5, а именно, f(× ) и g(× ) можно считать изображениями одной и той же сцены, если существует распределение цвета 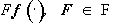, для которого v(j (× )) содержит f(× ) и g(× ). Есл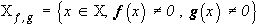и , и 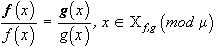, то, очевидно, существует 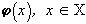, при котором f(x)Î v(j (× )), g(x)Î v(j (× )), а именно, 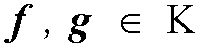, , 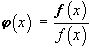если 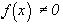, , 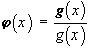если 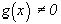, и, наконец, 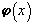- произвольно, если .

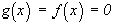На практике удобнее использовать другой подход, позволяющий одновременно решать задачи совмещения изображений и выделения объектов. Можно ли, например, считать g(× ) изображением сцены, представленной изображением f(× )? Ответ следует считать утвердительным, если

.

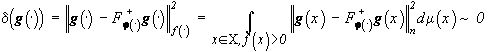Здесь j (× ) - распределение цвета на изображении f(× ), символ ~0 означает, что значение d (g(× )) можно объяснить наличием шума, каких-либо других погрешностей, или, наконец, - наличием или, наоборот, отсутствием объектов объясняющим несовпадение g(× ) и f(× ) с точностью до преобразования распределения яркостей. Такие объекты, изменившие распределение цвета g(× ) по сравнению с распределением цвета f(× ), представлены в .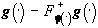

2).Идентификация при произвольном изменении распределения интенсивности и пространственно однородном изменении спектрального состава освещения.

Можно ли считать изображением сцены, представленной на изображении f(× ), изображение, полученное при изменившихся условиях регистрации, например, перемещением или изменением теней и изменением спектрального состава освещения?

Пусть - форма в широком смысле изображения f(× ), определенная в теореме @, П* - форма f(× ). Тогда ответ на поставленный вопрос можно считать утвердительным, если 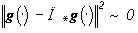. Если изменение g(× ) обусловлено не только изменившимися условиями регистрации, но также появлением и (или) исчезновением некоторых объектов, то изменения, обусловленные этим последним обстоятельством будут представлены на .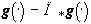

3). Задачи совмещения изображений и поиска фрагмента.

Пусть f(× ) - заданное изображение, AÌ X - подмножество поля зрения, c A(× ) - его индикатор, c A(× )f(× ) -назовем фрагментом изображения f(× ) на подмножестве A, представляющем выделенный фрагмент сцены, изображенной на f(× ). Пусть g(× ) - изображение той же сцены, полученное при других условиях, в частности, например, сдвинутое, повернутое, т.е. геометрически искаженное по сравнению с f(× ). Задача состоит в том, чтобы указать на g(× ) фрагмент изображения, представляющий на f(× ) фрагмент сцены и совместить его с c A(× )f(× ).

Ограничимся случаем, когда упомянутые геометрические искажения можно моделировать группой преобразований R2->R2, преобразование изображения 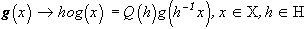назовем сдвигом g(× ) на h. Здесь

Q(h): Rn->Rn, hÎ H, - группа операторов. Векторный сдвиг на h¢ Î H даст

.

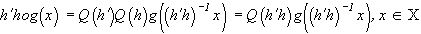В задаче выделения и совмещения фрагмента рассмотрим фрагмент сдвинутого на h изображения g(× ) в “окне” A:

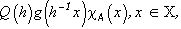(100)

причем, поскольку 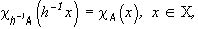где 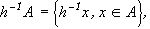то в (100) 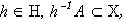- ограничение на сдвиг “окна” А, которое должно оставаться в пределах поля зрения X.

Если кроме цвета g(× ) может отличаться от f(× ), скажем, произвольным преобразованием распределения яркости при неизменном распределении цвета и 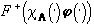- форма фрагмента f(× ), то задача выделения и совмещения фрагмента сводится к следующей задаче на минимум

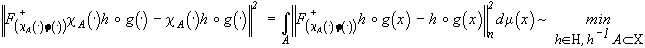.(101)

При этом считается, что фрагмент изображения g(× ), соответствующий фрагменту c A(× )f(× ), будет помещен в “окно”.А путем соответствующего сдвига h=h*, совпадает с c A(× )f(× ) с точностью до некоторого преобразования распределения яркости на нем. Это означает, что

.

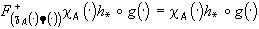т.е. в (101) при h=h* достигается минимум.

Рекомендуем скачать другие рефераты по теме: оформление доклада титульный лист, понятие культуры.



Предыдущая страница реферата | 5  6  7  8  9  10  11  12  13  14  15 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки