Предыдущая страница реферата | 5  6  7  8  9  10  11  12  13  14  15 | Следующая страница реферата

из условия минимума невязки по 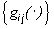. После этого для каждого i=1,...,N векторы 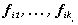должны быть определены из условия

(**)

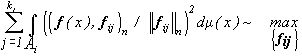при дополнительном условии ортогональности

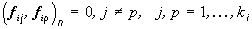. Решение этой задачи дается в следующей лемме

Лемма 5. Пусть 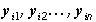ортогональные собственные векторы оператора Фi (23), упорядоченные по убыванию собственных значений:

.

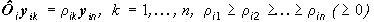Тогда решение задачи (**) дается равенствами .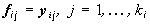

Доказательство. Заметим, что, поскольку Фi - самосопряженный неотрицательно определенный оператор, его собственные значения неотрицательны, а его собственные векторы всегда можно выбрать так, чтобы они образовали ортогональный базис в Rn. Пусть Pi - ортогонально проецирует в Rn на линейную оболочку 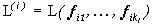собственных векторов 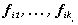и

[Pi Фi Pi] - сужение оператора Pi Фi Pi на 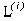. Тогда левая часть (*) равна следу оператора [Pi Фi Pi]

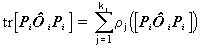, где 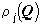- j-ое собственное значение оператора 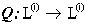(см., например, [10]). Пусть 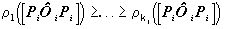. Тогда согласно теореме Пуанкаре, [10], 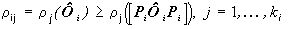, откуда следует утверждаемое в лемме. ¦

Воспользовавшись выражениями (*) и леммой 5, найдем, что в рассматриваемом случае имеет место утверждение, аналогичное теореме 3.

Теорема 3*. Наилучшее приближение любого изображения f(× ) изображениями (17*) имеет вид

,

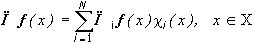Где 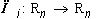: ортогональный проектор на линейную оболочку 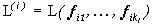, собственных векторов задачи

.

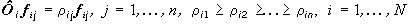Невязка наилучшего приближения равна

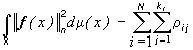.n

Рассмотрим теперь задачу наилучшего приближения изображения f изображениями (17), в которых заданы и фиксированы векторы 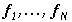, и надлежит определить измеримое разбиение 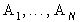и функции 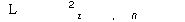, как решение задачи

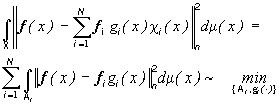(30)

При любом разбиении 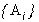минимум в (30) по 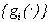достигается при 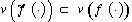, определяемых равенством (20). В свою очередь, очевидно, что

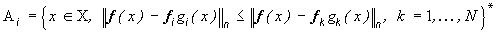(31)

где точки 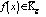, в которых выполняется равенство 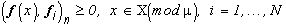могут быть произвольно включены в одно из множеств : либо в 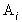, либо в 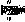. Это соглашение отмечено звездочкой в (31).

Таким образом доказана

Теорема 6. Пусть 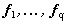заданные векторы Rn. Решением задачи (30) является изображение

,

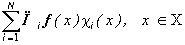Рекомендуем скачать другие рефераты по теме: оформление доклада титульный лист, понятие культуры.



Предыдущая страница реферата | 5  6  7  8  9  10  11  12  13  14  15 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки