Определитель произведения прямоугольных матриц. Теорема Коши-Бине.

Курсовая работа

Выполнила студентка  II курса группы ПМИ Решоткина Наталья Николаевна

Мурманский Государственный Педагогический Университет

Мурманск 2007

Введение

При решении различных задач математики очень часто приходится иметь дело с таблицами чисел, называемых матрицами. С помощью матриц удобно решать системы линейных уравнений, выполнять многие операции с векторами, решать различные задачи компьютерной графики и другие инженерные задачи.

Цель данной работы: теоретическое обоснование и необходимость практического применения теоремы Коши-Бине:

Пусть , -  и -матрицы соответственно, и

Тогда

Другими словами, при  определитель матрицы  является суммой произведений всевозможных миноров порядка  в  на соответствующие миноры матрицы  того же самого порядка

Работа состоит из четырех глав, содержит заключение, список литературы и приложение программы для теоремы Коши-Бине. В главе I рассматриваются элементы линейной алгебры – матрицы, операции над матрицами и свойства сложения матриц, и умножения на скаляр. Глава II посвящается умножению матриц и его свойств, а также транспонирование произведения двух матриц. В главе III рассматриваются обратимые и элементарные матрицы. В главе IV вводиться понятие определителя квадратной матрицы, рассматриваются свойства и теоремы об определителях, а также приводится доказательство теоремы Коши-Бине, что является целью моей работы. В дополнение прилагается программа показывающая механизм нахождения определителя произведения двух матриц.

Глава I

§ 1 Определение, обозначения и типы матриц

Мы определяем матрицу как прямоугольную таблицу чисел:

Где элементы матрицы aij (1≤i≤m, 1≤j≤n)-числа из поля .Для наших целей поле  будет либо множеством всех вещественных чисел, либо множеством всех комплексных. Размер матрицы , где m-число строк, n-число столбцов. Если m=n, то говорят, что матрица квадратная, порядка n. В общем случаем матрица называется прямоугольной.

Каждой  матрице  с элементами aij соответствует n×m матрица с элементами aji . Она называется транспонированной к  и обозначается через. Видно, что =. Строки матрицы  становятся столбцами в  и столбцы матрицы  становятся строками в.

Матрица называется нулевой если все элементы равны 0:

Матрица называется треугольной если все ее элементы, расположенные ниже главной диагонали равны 0

Треугольная матрица называется диагональной, если все элементы расположенные вне главной диагонали равны 0

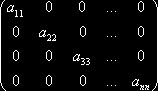
Диагональной матрица называется единичной, если все элементы расположенные на главной диагонали равны 1

Рекомендуем скачать другие рефераты по теме: доклад 6 класс, здоровый образ жизни реферат.



1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки