Предыдущая страница реферата | 3  4  5  6  7  8  9  10  11  12  13 | Следующая страница реферата

Чтобы доказать, что φ — взаимно однозначное отображение, построим обратное отображение ψ: T(m, q–1) → T(m, q), прочитав правило, задающее φ, слева направо:

ψ(r1, ..., ra | s1, ..., sb) =

  

(r1+1, ..., ra+1, 1 | s1–1, ..., sb–1), если sb > 0, (r1+1, ..., ra+1 | s1–1, ..., sb–1–1), если sb = 0.

Построенные отображения взаимно обратны, поэтому φ — взаимно однозначное соответствие. Значит, t(m, q) = t(m, q–1), что и утверждалось.

Чтобы научиться вычислять значения N(x, y), установим связь между числами t(m, q) и p(m).

Утверждение: t(m, q) = p(m).

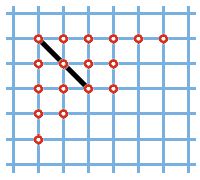
Рис. 4.

Мы уже знаем, что t(m, q) = t(m, 0), поэтому достаточно доказать, что t(m, 0) = p(m). Воспользуемся простым и полезным графическим средством, называемым диаграммой Юнга разбиения. Рассмотрим, например, разбиение (6, 4, 4, 2, 1). Его диаграмма Юнга изображена на рис. 4 (в первой строчке стоят 6 точек, во второй — 4, в третьей — 4, в четвёртой — 2, в пятой — 1). Всякое разбиение можно изобразить в виде диаграммы Юнга и по всякой диаграмме Юнга — записать разбиение.

Проведём на диаграмме Юнга диагональ — чёрная линия на рис. 4. Пусть r1 — число точек в первой строке, лежащих на диагонали и справа от неё, r2 — число точек второй строки, лежащих на диагонали и справа от неё, и т.д.; s1 — число точек первого столбца под диагональю, s2 — число точек второго столбца под диагональю и т.д. Поставим в соответствие диаграмме Юнга, изображающей разбиение числа m, пару последовательностей

(r1, r2, ... | s1, s2, ...),

r1 + r2 + ... + s1 + s2 + ... = m,

т.е. элемент множества T(m, 0). Например, диаграмме на рис. 4 соответствует пара (6, 3, 2 | 4, 2, 0). Зная пару последовательностей, можно легко восстановить диаграмму Юнга. Следовательно, мы установили взаимно однозначное соответствие между множеством разбиений и множеством T(m, 0). Утверждение доказано.

Теперь ничего не стоит ответить и на последний вопрос задачи — о значении N(13, 18). Поскольку 13 = 3+5·4/2, 18 = 3+6·5/2, точка (13, 18) лежит на третьей параболе. Значит, N(13, 18) = t(3, 0) = p(3) = 3.

Следующие упражнения — на применение диаграмм Юнга.

Упражнения

7. Число разбиений n не более чем с k частями, равно числу разбиений n с частями, не превосходящими k. Подсказка: отразите диаграмму Юнга относительно диагонали.

8. Число разбиений n с различными нечётными частями равно числу разбиений n, диаграмма Юнга которых симметрична относительно диагонали. Подсказка: вспомните соответствие Сильвестра.

Формула Гаусса–Якоби

Рекомендуем скачать другие рефераты по теме: проблема дипломной работы, шпаргалки по русскому.



Предыдущая страница реферата | 3  4  5  6  7  8  9  10  11  12  13 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки