Предыдущая страница реферата | 3  4  5  6  7  8  9  10  11  12  13 | Следующая страница реферата

$ бесконечное множество ненулевых решений этой системы (нулевое решение не определяет прямую). При этом для " решения (С1,С2,С3) справедливо равенство:

Т.е. решения системы (5) образуют единственный класс ненулевых троек. Этот класс определяет единственную прямую С.ч.т.д.

Теорема 2: Две различные прямые имеют единственную общую точку.

Доказательство: Пусть, С={(С1,С2,С3)}, m={(m1,m2,m3)} две различные прямые. Найдем () Х ={(Х1,Х2,Х3)}, лежащую на этих прямых. Достаточно повторить доказательство предыдущей теоремы, заменив Х на С, Y на m, С на Х. Получим, что единственная общая точка Х определяется равенством

Х=С*m (6).ч.т.д.

Теорема 3: Для того, чтобы три () Х,Y,Z лежали на одной прямой, необходимо и достаточно, чтобы

|X,Y,Z|=0 (7), то есть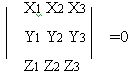

Доказательство: 1)Необходимость. Пусть () X,Y,Z лежат на одной прямой С. если хотя бы две из них совпадают, то равенство (7) следует из определения смешенного произведения и свойств определителя. Пусть эти () различны. Пользуясь теоремой 1, можно записать C=X*Y. Так как ()Z лежит на прямой C, то CZ=0 Þ (X*Y)Z=|X,Y,Z|=0

2)Достаточность. Пусть выполняется равенство (7). Рассмотрим произведение C=X*Y. Равенство (7) можно записать в виде (X*Y)Z=0, то есть CZ=0 Þ ()z лежит на прямой C проходящей через () X и Y. Равенство (7) не зависит от выбора представителей точек.

Теорема доказана.

Теорема 4: Для того, чтобы три прямые c, m, n проходили через одну () необходимо и достаточно, чтобы

|c,m,n|=0(8)

Для троек действительных чисел понятие линейной зависимости и линейной независимости определяется так же, как и для векторов. Пусть тройки x,…, x линейно зависимы. Легко проверить, что " другие тройки x,…, x, принадлежащие тем же классам, тоже линейно зависимы. Поэтому классы троек (точки) линейно зависимы, если линейно зависимы какие-нибудь представители этих классов.

Из теорем 3 и 4 следуют две теоремы.

Теорема 5: Для того, чтобы три () лежали на одной прямой, необходимо и достаточно, чтобы они были линейно зависимы.

Теорема 6: Для того, чтобы три прямые проходили через одну (), необходимо и достаточно, чтобы они были линейно зависимы.

2.3. Теорема Дезарга.

На проективной действительной плоскости имеет место теорема Дезарга.

Теорема Дезарга: Если прямые проходящие через соответствующие вершины двух трехвершинников пересекаются в одной точке, то точки пересечения соответствующих сторон этих трехвершинников лежат на одной прямой.

P=ABÇ A'B',Q=ACÇ A'C',R=BCÇ B'C',AA'Ç BB'Ç CC'=Q

P,Q,R лежат на одной прямой.

Доказательство: Введем проективную систему координат, примем () А,В,С,О за фундаментальные:

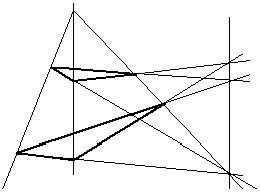
А(1,0,0), В(0,1,0), С(0,0,1), О(1,1,1)

Координаты ()А'- есть линейная комбинация координат ()А и ()О, так как А¹ А', то а'=a А + d q

Можно положить d =1. Тогда получаем А'=a А +q . Тоже самое относится и к другим вершинам трехвершинника A'B'C'. Поэтому А'(a +1,1,1), В'(1,b +1,1), С'(1,1,g +1) уравнение прямой АВ:

Рекомендуем скачать другие рефераты по теме: конспект урока 8 класс, шпаргалка егэ.



Предыдущая страница реферата | 3  4  5  6  7  8  9  10  11  12  13 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки