Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

Будем обозначать его Х={(Х1,Х2,Х3)}

Множество всех проективных точек называется действительной проективной плоскостью.

Определение 2: Проективной прямой называется множество всех точек удовлетворяющих линейному однородному уравнению вида:

С1Х 1+ С2Х 2+ С3Х 3=0(1)

где хотя бы одно из чисел Ci отлично от нуля.

Определение 2 корректно, так как если тройка (Х1,Х2,Х3) удовлетворяет уравнению (1), то в силу его однородности при любом действительном l тройка (l Х1, l Х2, l Х3) удовлетворяет уравнению (1).

Точки, удовлетворяющие уравнению (1) удовлетворяют также линейному однородному уравнению.

(m С1)Х 1+ (m С2)Х 2+ (m С3)Х 3=0(2)

при " m Î R: m ¹ 0.

Поэтому каждой прямой, заданной уравнением (2) можно поставить во взаимно однозначное соответствие класс пропорциональных троек С={(С1,С2,С3)}. Так, что тройками из одного класса соответствует одна прямая, причем этот класс не содержит нулевой тройки. Ввиду этого прямую, заданную уравнением (2) будем обозначать той же буквой С, что и соответствующий класс {(С1,С2,С3)}.

Равенство (2) можно записать также в виде

СХ=0(3)

Скалярное произведение троек С и Х. СХ= C1Х1 + С2Х2 + С3Х3 =0

Замечание: Рассмотрим 3-мерное линейное пространство L3. Исключим из него нулевой вектор 0. Множество L3{0} разобьем по классам эквивалентности так, что векторы одного класса коллинеарны между собой. Каждый такой класс назовем проективной точкой, а множество всех классов 2-мерным проективным пространством (плоскостью). Множество всех классов, векторы которых принадлежат { 0} назовем одномерной проективной плоскостью (прямой).

В L3 введем координаты. Тогда каждому вектору соответствует строка (Х1,Х2,Х3), а каждому классу эквивалентности из L3{ 0} (т.е. проективной ())- класс {(Х1,Х2,Х3)} пропорциональных строк, не содержащий нулевой строки.

Мы пришли к определению проективной плоскости.

2.2. Свойства проективной плоскости.

Докажем несколько простых теорем о взаимном расположении () и прямых на проективной плоскости.

Теорема 1: Через две различные () проходит единственная прямая.

Доказательство: 1) Существование. Пусть Х= {(Х1,Х2,Х3)} и У={(Y1,Y2,Y3)} две различные (). Определим прямую следующим образом:

C= Х*Yто естьС =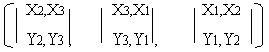

так какCХ = (Х*Y)Х = |Х,Y,Х| = 0

CY = (Х*Y)Y = |Х,Y,Y| = 0

и по свойству определителей, то () Х и Y принадлежат прямой С.

2). Единственность. Если прямая С={(C1,C2,C3)} содержит () Х и Y, то любой представитель (C1,C2,C3) класса С удовлетворяет системе уравнений.

(5)

Рекомендуем скачать другие рефераты по теме: конспект урока 8 класс, шпаргалка егэ.



Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки