Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

aA - cC = c'C' - a'A' (2)

А,С,Q- линейно зависимы Þ ()А,С,Q Î одной прямой.

А',С',Q'- линейно зависимы Þ ()А',С',Q' Î одной прямой.

Следовательно, Q=АСÇ А'С'

bB - cC = c'C' - b'B' = R (3)

В,С,R –линейно зависимы Þ ()В,С,R Î одной прямой.

В',С',R' –линейно зависимы Þ ()В',С',R' Î одной прямой

Следовательно, R=ВСÇ В'С'.

Составим выражение:

- векторы линейно зависимы Þ ()P,Q,R лежат на одной прямой.

Теорема доказана.

Принято называть трехвершинники, удовлетворяющие теореме Дезарга, дезарговыми. ()О=АА'Ç ВВ'Ç СС'- дезарговой, прямую, которой принадлежат точки P,Q,R - дезарговой. Для теоремы Дезарга имеет место обратная теорема:

Если точки пересечения соответственных сторон двух трехвершинников лежат на одной прямой, то прямые, проходящие через соответственные вершины этих трехвершинников, проходят через одну точку.

Замечание: Трехвершинник - это фигура, которая состоит из трех точек не лежащих на одной прямой и прямых проходящих через каждую пару этих точек.

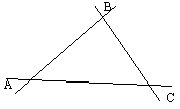
А,В,С- вершины прямые АВ,ВС,АС- стороны

1.5. Теорема Паппа.

Следующей составляющей данной теории является теорема Паппа- Паскаля, которая является частным случаем теоремы Паскаля. Сформулируем теорему Паскаля.

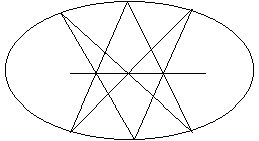
рис. 1

Теорема Паскаля: Для того, чтобы шесть точек, из которых никакие три не лежат на одной прямой принадлежали овальной кривой, необходимо и достаточно, чтобы точки пересечения соответствующих сторон шестивершинника* лежали на одной прямой. AB’Ç A’B=P,AC’Ç A'C=Q, BC’Ç B’C=R.(рис. 1)

P,Q,R принадлежат прямой (прямая Паскаля)

Рассмотрим теорему Паскаля в том частном случае, когда кривая второго порядка распадается на пару прямых. Пусть А,В,С,А',В',С'- шесть вершин шестиугольника Паскаля, расположенных по три на данных прямых l и l', которые мы рассматриваем как распавшуюся кривую второго порядка (рис 2). Тогда имеем следующие три точки пересечения пар соответствующих сторон шестиугольника: Р=АВ'Ç А'В, Q=А'СÇ АС', R=ВС'Ç В'С. По теореме Паскаля эти три точки лежат на одной прямой. Рассмотренный частный случай теоремы Паскаля был известен древним греческим геометрам и носил название теоремы Паппа. Теперь эта теорема носит название Паппа - Паскаля.

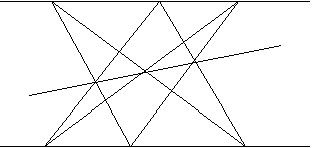
Рис. 2

*шестивершинником называется фигура состоящая из последовательности шести ()А1, А2, А3, А4, А5, А6 называемых вершинами и шести прямых А1А2, А2А3, А3А4, А4А5, А5А6, А6А1 называемых сторонами.

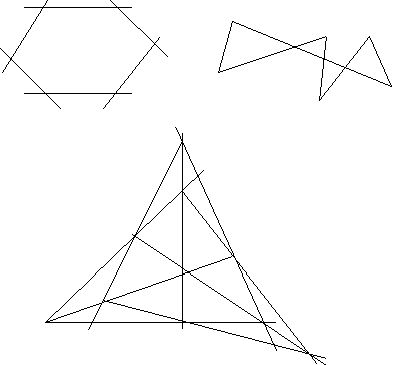
Мы рассмотрели один из подходов к определению проективной плоскости, а именно определения проективной плоскости на базе трехмерного векторного пространства.

Теперь рассмотрим аналитическое определение проективной плоскости.

Глава 2. Аналитическое построение проективной плоскости. 2.1. Понятие проективной плоскости.

Определение 1: Проективной точкой называется класс пропорциональных троек действительных чисел, не содержащих нулевой тройки.

Рекомендуем скачать другие рефераты по теме: конспект урока 8 класс, шпаргалка егэ.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки